Bạn đang xem bài viết Hàm số nghịch biến khi nào? Lý thuyết và bài tập tại Thcslytutrongst.edu.vn bạn có thể truy cập nhanh thông tin cần thiết tại phần mục lục bài viết phía dưới.
Một trong những khái niệm quan trọng trong toán học là hàm số. Với mỗi hàm số, ta có thể xác định được sự biến đổi của giá trị của hàm số khi thay đổi giá trị đầu vào. Trong bài viết này, chúng ta sẽ tìm hiểu về một loại đặc biệt của hàm số, được gọi là hàm số nghịch biến.
Đầu tiên, hãy hiểu rõ về khái niệm của hàm số nghịch biến. Một hàm số được gọi là nghịch biến trên một khoảng nếu khi một giá trị của biến độc lập tăng, thì giá trị của hàm số giảm, và ngược lại. Điều này có nghĩa là đồ thị của hàm số nghịch biến sẽ có dạng “đi xuống” khi ta đi từ trái sang phải.
Tuy nhiên, để xác định được một hàm số nghịch biến, chúng ta cần phải biết về tính chất của hàm số và cách tính đạo hàm. Hàm số được gọi là nghịch biến trên một khoảng nếu đạo hàm của nó luôn có dấu trái ngược với tăng giảm của biến độc lập trên khoảng đó. Nghĩa là, khi ta tăng giá trị của biến độc lập, đạo hàm sẽ giảm và ngược lại.
Để hiểu rõ hơn về lý thuyết này, hãy cùng xem qua một số bài tập về hàm số nghịch biến. Bài tập này nhằm giúp bạn làm quen với việc áp dụng lý thuyết và tính toán các đạo hàm để xác định tính chất của hàm số.
1. Xác định xem hàm số y = 2x – 3 có phải là nghịch biến hay không trên khoảng [-∞, +∞].
2. Tìm tất cả các giá trị của tham số a để hàm số y = ax^3 – 3x^2 + 2x là nghịch biến trên khoảng [-1, 2].
3. Xác định tất cả các giá trị của h để hàm số y = hx^2 + 4x – 2x^3 là nghịch biến trên khoảng r.
Như vậy, qua bài viết này, chúng ta đã hiểu về khái niệm và tính chất của hàm số nghịch biến. Bằng cách sử dụng lý thuyết và tính toán đạo hàm, ta có thể xác định được tính chất của hàm số. Hy vọng những bài tập trên đã giúp bạn nắm vững kiến thức về chủ đề này.
Dạng toán hàm số nghịch biến thường xuất hiện nhiều trong các đề thi THPTQG và trong các đề thi thử của các trường trên toàn quốc. Nhiều bạn vẫn thắc mắc Hàm số nghịch biến khi nào? Điều kiện của nó là gì? Bài viết này của Chúng Tôi sẽ giải đáp và giúp các bạn ôn tập tốt dạng toán này!
Định nghĩa hàm số nghịch biến
Hàm số nghịch biến, đồng biến hay còn gọi là hàm số đơn điệu.
Cho K là một khoảng, một đoạn hoặc một nửa khoảng và y = f(x) là một hàm số xác định trên K.
Hàm số y = f(x) được gọi là nghịch biến (giảm) trên K, nếu:
- ∀ x1, x2 ∊ K mà x1 < x2 thì f (x1) > f (x2)
- Biểu diễn đồ thị hàm số là một đường đi xuống.
Hàm số nghịch biến khi nào?
Hàm số f nghịch biến trên K khi và chỉ khi:
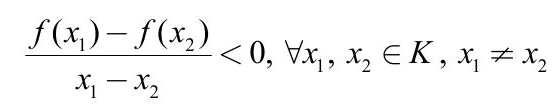
Điều kiện đủ để hàm số nghịch biến
Cho hàm số f có đạo hàm trên K.
Nếu f'(x) < 0 với mọi x ∈ K thì f nghịch biến trên K.
Định lí mở rộng
Chỉ xét K là một khoảng
Giả sử hàm số f có đạo hàm trên K
Nếu f'(x) ≤ 0 với mọi x ∈ K và f'(x) = 0 chỉ tại một số hữu hạn điểm thuộc K thì f nghịch biến trên K.
Phương pháp xét tính đơn điệu của hàm số
- Tìm tập xác định
- Tính đạo hàm f'(x). Tìm các điểm xi (i= 1 , 2 ,…, n) mà tại đó f'(x) bằng 0 hoặc không xác định.
- Sắp xếp các điểm xi theo thứ tự tăng dần và lập bảng biến thiên.
- Nêu kết luận về các khoảng đồng biến, nghịch biến của hàm số.
Bài tập mẫu
Dạng toán xét sự đồng biến, nghịch biến của hàm số

Kết luận: Hàm số đồng biến trên các khoảng (-∞;2) và (4;+∞), nghịch biến trên khoảng (2;4).

Dạng toán tìm m để hàm số nghịch biến
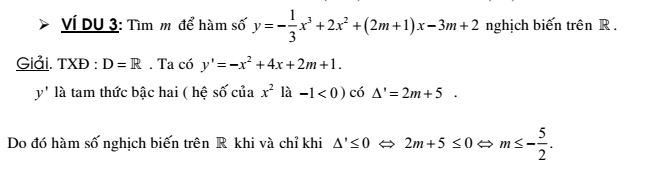
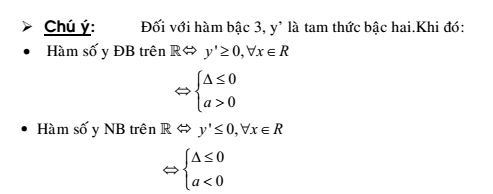
Ví dụ 4: Tìm m để hàm số: ![]() nghịch biến trong khoảng (-1/2;1/2)
nghịch biến trong khoảng (-1/2;1/2)

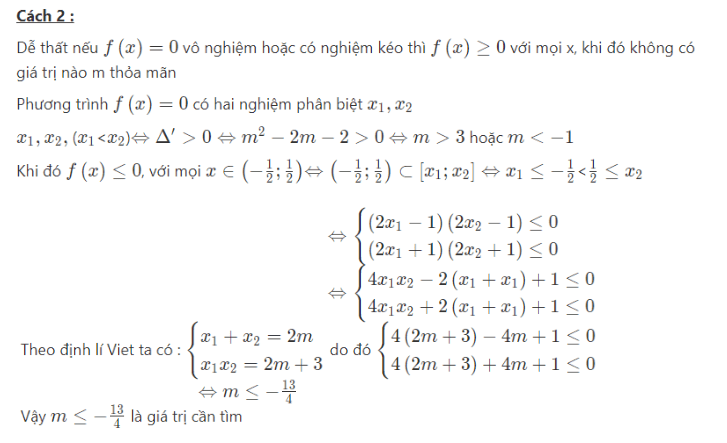
Qua những kiến thức trên mà Chúng Tôi chia sẻ, hy vọng bạn đọc sẽ nắm vững kiến thức về hàm số nghịch biến khi nào và ôn tập thật tốt. Chúc các bạn thành công!
Kết luận cho chủ đề “Hàm số nghịch biến khi nào? Lý thuyết và bài tập”:
Trong lĩnh vực toán học, hàm số nghịch biến là một loại hàm mà giá trị của nó giảm khi độc lập tăng và tăng khi độc lập giảm. Điều này có nghĩa là khi một biến tăng, giá trị của hàm số giảm, và khi biến giảm, giá trị của hàm số tăng.
Để xác định một hàm số có nghịch biến hay không, ta có thể sử dụng một số phương pháp đơn giản như tính đạo hàm hoặc vẽ đồ thị hàm số.
Theo lý thuyết, một hàm số f(x) được gọi là nghịch biến trên một khoảng [a, b] nếu và chỉ nếu f(x) âm và f(y) dương khi độc lập x và y thoả mãn a
Cảm ơn bạn đã xem bài viết Hàm số nghịch biến khi nào? Lý thuyết và bài tập tại Thcslytutrongst.edu.vn bạn có thể bình luận, xem thêm các bài viết liên quan ở phía dưới và mong rằng sẽ giúp ích cho bạn những thông tin thú vị.
Từ Khoá Liên Quan:
1. Hàm số nghịch biến là gì?
2. Đặc điểm của hàm số nghịch biến.
3. Điều kiện để hàm số nghịch biến.
4. Đồ thị của hàm số nghịch biến.
5. Hàm số đồng biến và nghịch biến.
6. Quy tắc vi phân hàm số nghịch biến.
7. Hình dạng đồ thị của hàm số nghịch biến.
8. Phương trình hàm số nghịch biến.
9. Ví dụ về hàm số nghịch biến.
10. Hàm số nghịch biến trong thực tế.
11. Hàm số nghịch biến trong lý thuyết đồ thị.
12. Hàm số nghịch biến và đường tiệm cận.
13. Bài tập về hàm số nghịch biến.
14. Các tính chất của hàm số nghịch biến.
15. Ứng dụng của hàm số nghịch biến trong giải toán.


