Cách chứng minh hình bình hành? Khái niệm, tính chất, dấu hiệu HBH

Khái niệm về hình bình hành có lẽ chẳng còn xa lạ gì đối với mỗi người. Nếu bạn đã quên mất cách chứng minh hình bình hành, hãy cùng Chúng Tôi ôn lại trong nội dung bài viết dưới đây.

Hình bình hành là gì?

Hình bình hành là gì?

Hình bình hành là tứ giác mà có 2 cặp cạnh đối song song với nhau hoặc 1 cặp cạnh đối song song và bằng nhau. Hình bình hành là một trường hợp đặc biệt của hình thang.

Ví dụ: Cho hình bình hành MNPQ từ đó ta sẽ được cặp: MN//PQ và MQ//NP.

Dấu hiệu nhận biết hình bình hành

Sau đây là những dấu hiệu nhận biết hình bình hành

• Tứ giác có các cạnh đối song song là hình bình hành.
• Tứ giác có các cạnh đối bằng nhau là hình bình hành.
• Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.
• Tứ giác có các góc đối bằng nhau là hình bình hành.
• Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành.
• Hình thang có hai cạnh đáy bằng nhau là hình bình hành.

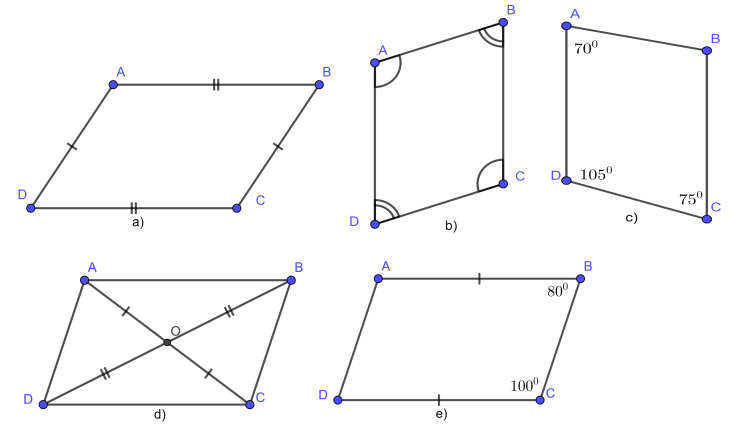
Tính chất hình bình hành

Tính chất hình bình hành được thể hiện như sau:

• Các cạnh đối song song và bằng nhau.
• Các góc đối bằng nhau.
• Hai đường chéo cắt nhau tại trung điểm của mỗi đường.

Cách chứng minh hình bình hành

Tứ giác có các cạnh đối song song

Cách chứng minh hình bình hành qua các cạnh đối song song

Ví dụ: Cho tứ giác ABCD như hình dưới đây:

• Điểm E là trung điểm của đoạn thẳng AB.
• Điểm F là trung điểm của đoạn thẳng BC.
• Điểm G là trung điểm của đoạn thẳng DC.
• Điểm H là trung điểm của đoạn thẳng AD.

Các bạn hãy cho biết tứ giác EFGH là hình gì? Chứng minh điều đó?

Bài làm:

Sau khi vẽ hình và nhìn vào hình vẽ, chúng ta có:

• EF là đường trung bình của tam giác ABC, nên ta suy ra được EF // AC.
• HG là đường trung bình của tam giác ADC, nên ta suy ra được HG // AC.
• Từ hai dữ liệu trên chúng ta có thể biết được rằng EF//HC.

Tiếp theo chúng ta có:

• FG là đường trung bình của tam giác BDC, nên FG // BD.
• EH là đường trung bình của tam giác BDA, nên EH // BD.
• Từ dữ liệu trên chúng ta có thể biết được cạnh FG // EH.

Chúng ta xét tứ giác EFGH và thấy được rằng cạnh EF // HG và FG // EH.

Hình tứ giác EFGH là hình bình hành vì nó có hai cặp cạnh đối song song (điều phải chứng minh)

Tứ giác có các cạnh đối bằng nhau

Cách chứng minh hình bình hành qua các cạnh đối bằng nhau

Ví dụ: Cho Tứ giác ABCD có ∆ABC = ∆CDA. Chứng minh rằng ABCD là Hình bình hành.

Bài làm:

Theo bài ra, ta có:

∆ABC = ∆CDA => AD = BC và AB = CD

=> ABCD là hình bình hành dó có các cặp cạnh đối bằng nhau.

Tứ giác có hai cạnh đối song song và bằng nhau

Ví dụ: Cho hình bình hành ABCD, gọi E là trung điểm AD, F là trung điểm BC. Chứng minh rằng BEDF là hình bình hành.

Bài làm:

Ta có:

ABCD là hình bình hành => AD // BC và AD = BC

AD // BC => DE // BF (1)

E là trung điểm AD => DE = AD/2

F là trung điểm BC => BF = BC/2

Mà AD = BC (ABCD là hình bình hành)

DE = BF (2)

Từ (1) và (2) => Tứ giác DEBF là hình bình hành do có hai cạnh đối song song và bằng nhau.

Tứ giác có các góc đối bằng nhau

Ví dụ: Cho hình tứ giác ABCD có tam giác ABC = tam giác ADC, tam giác ADB = tam giác CDB. Hãy chứng minh tứ giác trên chính là hình bình hành?

Bài làm:

Dựa theo đề bài đã cho chúng ta có:

• Tam giác ABC= tam giác ADC nên góc B= góc D(1)
• Tam giác ADB = tam giác CDB nên góc A= góc C(2)

Từ 1 và 2 chúng ta có thể kết luận rằng tứ giác ABCD chính là hình bình hành vì nó có các góc đối bằng nhau.

Tứ giác có hai đường chéo cắt nhau tại mỗi trung điểm mỗi đường

Ví dụ: Cho hình bình hành ABCD có hai đường chéo AC và BD cắt nhau tại O. Kẻ thêm đường AE vuông góc với BD và CF vuông góc với BD. Hãy chứng minh rằng tứ giác AFCE là hình bình hành.

Bài làm:

Áp dụng tính chất của hình bình hành chúng ta có AO=OC(1).

Xét tam giác vuông AOE và AOF có:

Góc E= góc F= 90 độ vì góc AOE = góc AOF( hai đỉnh đối nhau)
Từ đó suy ra được tam giác AOE = tam giác COF nên cạnh OE=OF(2)

Từ(1) và (2) ta kết luận được rằng tứ giác AECE là hình bình hành vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường.

Xem thêm: Cách tính diện tích hình bình hành, ví dụ minh họa – Toán 4

Bài tập liên quan đến cách chứng minh hình bình hành

Bài 1: Cho hình bình hành ABCD (AB > BC). Tia phân giác của góc D cắt AB ở E, tia phân giác của góc B cắt CD ở F.

Bài làm:

a) Ta có :

Góc B = Góc D”> Góc B = Góc D (Vì ABCD”>ABCD là hình hành) (1)

Góc B1 = Góc B2 = Góc B2″> Góc B1 = Góc B2 (vì BF”> BF là tia phân giác góc B”> Góc B) (2)

Góc D1 = Góc D2 = Góc D2″> Góc D1 = Góc D2 (vì DE”>DE là tia phân giác góc D> Góc D) (3)

Từ (1), (2), (3) ⇒ Góc D2= Góc B1″>⇒ Góc D2 = Góc B1, mà hai góc này ở vị trí so le trong do đó: DE//BF”>DE//BF (*)

b) Tứ giác DEBF có:

DE // BF (chứng minh ở câu a)

BE // DF (vì AB // CD)

Nên theo định nghĩa DEBF là hình bình hành.

Bài 2: Tứ giác ABCD có E, F, G, H theo thứ tự là trung điểm của các cạnh AB, BC, CD, DA. Tứ giác EFGH là hình gì? Vì sao?

Bài làm:

Tứ giác EFGH là hình bình hành.

EB = EA, FB = FC (gt) nên EF là đường trung bình của ∆ABC.

Do đó EF // AC

Tương tự HG là đường trung bình của ∆ACD.

Do đó HG // AC

Suy ra EF // HG       (1)

Tương tự EH // FG   (2)

Từ (1) và (2) suy ra EFGH là hình bình hành (dấu hiệu nhận biết 1).

Vừa rồi Chúng Tôi đã chia sẻ cho bạn cách chứng minh hình bình hành. Hy vọng bạn có thể vận dụng bài viết một cách chính xác nhất. Cùng Chúng Tôi cập nhật các kiến thức bổ ích khác qua các bài viết sau nha!