Bạn đang xem bài viết Bán kính đường tròn ngoại tiếp tam giác là gì? Khái niệm tại Thcslytutrongst.edu.vn bạn có thể truy cập nhanh thông tin cần thiết tại phần mục lục bài viết phía dưới.
Bán kính đường tròn ngoại tiếp tam giác là một khái niệm quan trọng trong lĩnh vực hình học. Khi nói về tam giác và đường tròn, chúng ta không thể không nhắc đến bán kính đường tròn ngoại tiếp. Điều này xuất phát từ việc tam giác có thể được nằm bên trong một đường tròn có bán kính nhất định. Tuy nhiên, không phải tất cả các tam giác đều có đường tròn ngoại tiếp và chính bán kính của đường tròn ngoại tiếp sẽ định nghĩa hình dáng và kích thước của tam giác. Vì vậy, để hiểu rõ về bán kính đường tròn ngoại tiếp tam giác, chúng ta cần khám phá sâu hơn về các quy tắc và công thức liên quan đến nó. Trên cơ sở đó, ta có thể áp dụng bán kính đường tròn ngoại tiếp trong nhiều vấn đề thực tiễn, từ xây dựng đến tính toán hình học, tạo nên sự hứng thú và ứng dụng đa dạng của chủ đề này.
Trong Toán học, đường tròn ngoại tiếp tam giác có thể coi là một trong những phần vô cùng quan trọng. Vậy thì để hiểu chi tiết hơn về bán kính đường tròn ngoại tiếp tam giác, các bạn hãy cùng Chúng Tôi đi vào khám phá ngay dưới đây nhé!
Đường tròn ngoại tiếp tam giác là gì?
Đường tròn ngoại tiếp tam giác là đường tròn đi qua ba đỉnh của tam giác. Từ đó, khi nối tâm O của đường tròn với ba đỉnh của tam giác ABC ta có được bán kính đường tròn ngoại tiếp của tam giác ABC là OA = OB = OC.
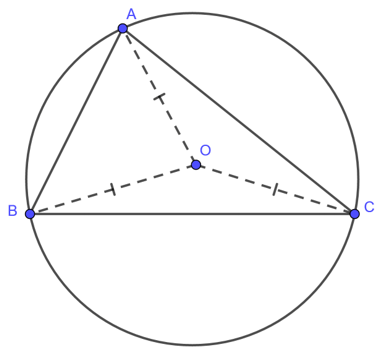
Tính chất của đường tròn ngoại tiếp tam giác:
- Mỗi tam giác sẽ chỉ có duy nhất một đường tròn ngoại tiếp.
- Tâm đường tròn ngoại tiếp tam giác là giao điểm của ba đường trung trực của tam giác đó.
- Tâm đường tròn ngoại tiếp tam giác vuông là trung điểm của cạnh huyền.
- Trong tam giác đều, tâm đường tròn ngoại tiếp và nội tiếp tam giác trùng nhau.
Công thức tính bán kính đường tròn ngoại tiếp tam giác
Các công thức tính bán kính đường tròn ngoại tiếp tam giác:
- Công thức tính bán kính đường tròn ngoại tiếp tam giác: R = (a x b x c) : 4S.
- Công thức tính bán kính đường tròn ngoại tiếp của góc A:
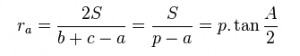
- Công thức tính bán kính đường tròn ngoại tiếp của góc B:
![]()
- Công thức tính bán kính đường tròn ngoại tiếp của góc C:
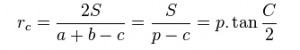
Trong đó:
- r: Bán kính đường tròn ngoại tiếp tam giác
- S: Diện tích tam giác.
- a, b, c: Độ dài các cạnh của hình tam giác.
- A, B, C: Các góc của hình tam giác.
Cách tính bán kính đường tròn ngoại tiếp tam giác
Có rất nhiều cách khác nhau để tính bán kính đường tròn ngoại tiếp tam giác. Sau đây là một số cách phổ biến.
Sử dụng định lí sin trong tam giác
Cách đầu tiên chính là sử dụng định lí sin trong tam giác để tính bán kính đường tròn ngoại tiếp tam giác.
Ví dụ: Cho tam giác ABC có BC = a, CA = b và AB = c, R là bán kính đường tròn ngoại tiếp tam giác ABC. Khi đó:
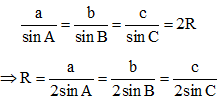
Trong đó có:
- R: Bán kính đường tròn ngoại tiếp tam giác
- a, b, c: Độ dài các cạnh của hình tam giác.
- A, B, C: Các góc của hình tam giác.
Sử dụng diện tích tam giác
Bên cạnh cách dùng định lý sin, chúng ta cũng có thể sử dụng diện tích trong tam giác để tính bán kính đường tròn ngoại tiếp tam giác:
![]()
Trong đó có:
- R: Bán kính đường tròn ngoại tiếp tam giác.
- S: Diện tích tam giác.
- a, b, c: Độ dài các cạnh của hình tam giác.
- A, B, C: Các góc của hình tam giác.
Sử dụng trong hệ tọa độ
Ngoài ra, tính bán kính đường tròn khi sử dụng trong hệ tọa độ cũng là một cách được rất nhiều người ưa chuộng. Sau đây là các bước cơ bản để tính bán kính:
- Tìm tọa độ tâm O của đường tròn ngoại tiếp tam giác ABC.
- Tìm tọa độ một trong ba đỉnh A, B, C (nếu chưa có).
- Tính khoảng cách từ tâm O tới một trong ba đỉnh A, B, C, đây chính là bán kính cần tìm: R=OA=OB=OC.
Sử dụng tam giác vuông
Sử dụng tam giác vuông để tính bán kính có lẽ là cách cơ bản nhất. Tâm của đường tròn ngoại tiếp trong tam giác vuông là trung điểm của cạnh huyền.
Do vậy, bán kính đường tròn ngoại tiếp tam giác vuông là bằng nửa độ dài của cạnh huyền đó.
Bài tập về bán kính đường tròn ngoại tiếp tam giác
Nhằm hiểu sâu hơn về bài học, chúng ta sẽ cùng nhau đi đến các bài tập về bán kính đường tròn ngoại tiếp tam giác.
Bài tập 1: Cho tam giác MNP vuông tại N, và MN = 6cm, NP = 8cm. Xác định bán kính đường tròn ngoại tiếp tam giác MNP bằng bao nhiêu?
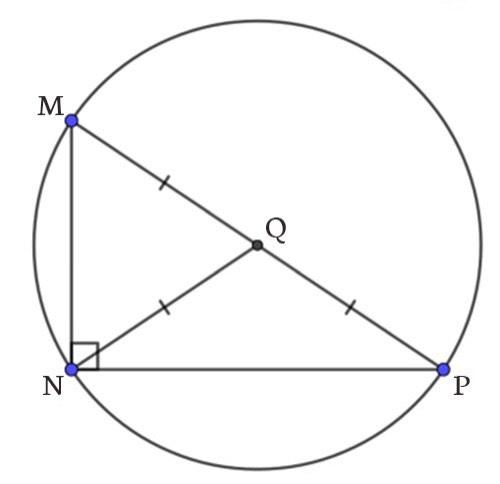
Áp dụng định lý Pytago, ta có:
PQ = 1/2 MP
=> NQ = QM = QP = 5cm
Gọi D là trung điểm MP.
=> ∆MNP vuông tại N có NQ là đường trung tuyến ứng với cạnh huyền MP
=> Q là tâm đường tròn ngoại tiếp ∆MNP
=> Đường tròn ngoại tiếp ∆MNP là trung điểm Q của cạnh huyền và bán kính đường tròn ngoại tiếp MNP là R = MQ = 5cm
Bài tập 2: Cho tam giác ABC có góc B bằng 45° và AC = 4. Tính bán kính đường tròn ngoại tiếp tam giác ABC.
Gọi R là bán kính đường tròn ngoại tiếp tam giác ABC.
Ta có: b = AC = 4
Áp dụng định lý sin trong tam giác ABC ta có:
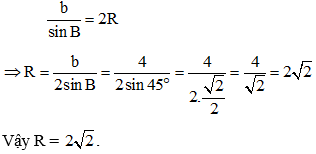
Bài tập 3: Cho tam giác MNP có MN = 6, MP = 8 và PN = 10. Tính bán kính đường tròn ngoại tiếp tam giác MNP.
Ta có: MN² + MP² = 6² + 8² = 36 + 64 = 100.
mà PN² = 10² = 100.
=> MN² + MP² = PN².
Do đó tam giác MNP vuông tại M (định lý Pytago đảo).
Vậy bán kính đường tròn ngoại tiếp tam giác MNP là :
R = 1/2 PN = 1/2.10 = 5.
Bài tập 4: Cho tam giác MNP đều với cạnh bằng 12cm. Xác định tâm và bán kính đường tròn ngoại tiếp ∆MNP?
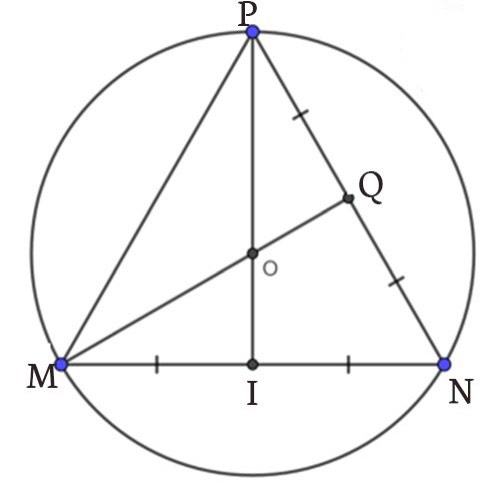
Gọi Q, I lần lượt là trung điểm của cạnh NP, MN và MQ giao với PI tại O.
Vì ∆MNP đều nên đường trung tuyến cũng là đường cao, đường phân giác, đường trung trực của tam giác.
=> O là tâm của đường tròn ngoại tiếp.
=> ∆MNP có PI là đường trung tuyến nên PI cũng là đường cao.
Từ đó áp dụng định lý Pytago:
PI² = MP² – MI² = 122 – 62 = 108 (cm).
=> PI = 6√3cm.
Bởi O là trọng tâm của ∆MNP nên:
PO = 2/3 PI = 2/3 x 6√3 = 4√3 (cm).
Như vậy qua bài viết trên, chắc hẳn các bạn cũng đã biết cách tính bán kính đường tròn ngoại tiếp tam giác rồi phải không nào? Vậy thì các bạn hãy mau chóng theo dõi Chúng Tôi ngay để cập nhật thêm nhiều thông tin thú vị hơn nữa nhé!
về bán kính đường tròn ngoại tiếp tam giác là một khái niệm cơ bản trong hình học. Bán kính đường tròn ngoại tiếp tam giác là độ dài đoạn thẳng nối trung điểm của các cạnh tam giác với tâm của đường tròn ngoại tiếp tam giác.
Qua việc nghiên cứu bán kính đường tròn tiếp tam giác, ta có thể nhận thấy rằng đây là một thuộc tính quan trọng của tam giác. Bán kính đường tròn ngoại tiếp tam giác có thể sử dụng để giải quyết các vấn đề liên quan đến tam giác, củng cố được một số kết quả và định lý hình học.
Một điểm đáng chú ý là bán kính đường tròn ngoại tiếp tam giác có thể được tính toán dễ dàng thông qua công thức Euler, trong đó bán kính bằng nửa chu vi của tam giác chia cho diện tích của tam giác. Điều này cho phép chúng ta dễ dàng xác định bán kính đường tròn tiếp tam giác chỉ từ các thông tin cơ bản như độ dài các cạnh tam giác.
Bên cạnh việc cung cấp thông tin về sự liên kết giữa bán kính và tam giác, bán kính đường tròn tiếp tam giác còn có thể áp dụng trong các bài toán thực tế. Ví dụ, trong xây dựng, bán kính đường tròn ngoại tiếp tam giác được sử dụng để tính toán và xác định vị trí các điểm trên mặt đất, giúp giảm thiểu sai số và đảm bảo tính chính xác trong quá trình xây dựng.
Tóm lại, bán kính đường tròn ngoại tiếp tam giác là một khái niệm quan trọng trong hình học, mang lại sự liên kết vững chắc giữa các yếu tố của tam giác và có ứng dụng trong thực tế. Hiểu và ứng dụng khái niệm này sẽ giúp ta tăng cường kiến thức và hiểu biết về hình học, cũng như áp dụng vào việc giải quyết các bài toán liên quan.
Cảm ơn bạn đã xem bài viết Bán kính đường tròn ngoại tiếp tam giác là gì? Khái niệm tại Thcslytutrongst.edu.vn bạn có thể bình luận, xem thêm các bài viết liên quan ở phía dưới và mong rằng sẽ giúp ích cho bạn những thông tin thú vị.
Từ Khoá Liên Quan:
1. Bán kính đường tròn ngoại tiếp tam giác
2. Bán kính đường tròn ngoại tiếp
3. Tam giác ngoại tiếp đường tròn
4. Đường tròn ngoại tiếp tam giác
5. Đường tròn ngoại tiếp tam giác vuông
6. Tam giác cân và đường tròn ngoại tiếp
7. Bán kính đường tròn ngoại tiếp tam giác đều
8. Bán kính đường tròn ngoại tiếp tam giác đặc biệt
9. Bán kính đường tròn ngoại tiếp tam giác vuông cân
10. Bán kính đường tròn ngoại tiếp tam giác tù
11. Bán kính đường tròn ngoại tiếp tam giác nhọn
12. Chu vi đường tròn ngoại tiếp tam giác
13. Tiếp tuyến đường tròn ngoại tiếp tam giác
14. Công thức tính bán kính đường tròn ngoại tiếp tam giác
15. Đối tượng nghiên cứu trong bán kính đường tròn ngoại tiếp tam giác


