Bạn đang xem bài viết Cách tính chu vi hình tam giác – Giải bài tập SGK Toán 3 tại Thcslytutrongst.edu.vn bạn có thể truy cập nhanh thông tin cần thiết tại phần mục lục bài viết phía dưới.
Có rất nhiều dạng bài tập trong sách giáo trình Toán lớp 3 liên quan đến tính chu vi hình tam giác. Đối với hình tam giác, việc tính chu vi là một trong những khái niệm cơ bản mà các học sinh cần nắm vững.
Trước khi làm bài tập về tính chu vi hình tam giác, chúng ta cần hiểu rõ về khái niệm chu vi. Chu vi hình tam giác chính là tổng độ dài của 3 cạnh của tam giác. Việc tính chu vi hình tam giác không quá khó, chỉ đòi hỏi chúng ta biết các công thức cơ bản và làm theo từng bước một.
Khi tính chu vi hình tam giác, chúng ta thường sẽ gặp các dạng bài tập khác nhau. Với tam giác đều, cạnh của tam giác có độ dài bằng nhau nên việc tính chu vi sẽ đơn giản hơn. Đối với tam giác vuông, chúng ta có thể sử dụng định lý Pythagore để tính độ dài cạnh và sau đó tính tổng các cạnh để tìm chu vi. Đối với tam giác thường, chúng ta cần biết độ dài các cạnh của tam giác để tính chu vi.
Trong quá trình tính chu vi hình tam giác, các em cũng cần chú ý các yếu tố như đưa đơn vị đo lường, như mét, centimet, vào kết quả cuối cùng và làm tròn đến đúng số chữ số yêu cầu trong đề bài.
Với việc nắm vững các công thức tính chu vi hình tam giác và ôn tập kỹ càng, chúng ta có thể trả lời các bài tập trong sách giáo trình Toán lớp 3 liên quan đến tính chu vi hình tam giác một cách dễ dàng.
Các dạng bài toán tính chu vi, diện tích hình tam giác, hình chữ nhật, hình vuông xuất hiện rất nhiều trong bài thi Toán cấp 1. Vậy để làm tốt bài tập, các bạn học sinh cần nắm rõ công thức tính chu vi, diện tích các hình.
Bài viết hôm nay của Chúng Tôi sẽ hướng dẫn bạn cách tính chu vi hình tam giác và các dạng bài tập có liên quan. Cùng theo dõi bạn nhé!
Cách tính chu vi hình tam giác
Có 4 loại tam giác cơ bản là tam giác thường, tam giác cân, tam giác vuông và tam giác đều. Mỗi dạng tam giác đều có cách tính chu vi khác nhau. Cùng tìm hiểu nhé!
Cách tính chu vi hình tam giác thường
Tam giác thường là loại tam giác cơ bản nhất, có độ dài các cạnh khác nhau, số đo góc trong cũng khác nhau.
Công thức tính chu vi hình tam giác thường: P = a + b + c
Trong đó:
- P là chu vi tam giác
- a, b, c lần lượt là độ dài 3 cạnh của tam giác
Diễn đạt bằng lời: Chu vi tam giác bằng độ dài tổng ba cạnh của tam giác đó.
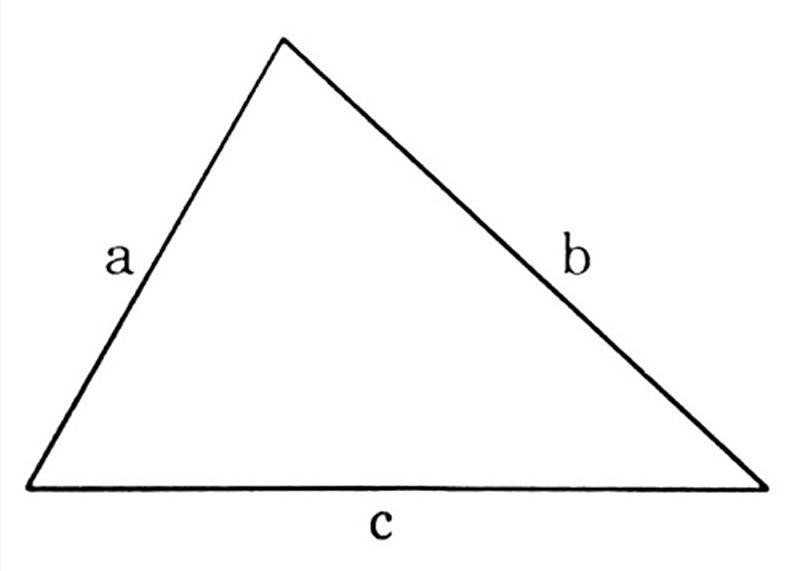
Ví dụ: Cho tam giác có độ dài 3 cạnh lần lượt là 4cm, 8cm và 9cm. Tính chu vi hình tam giác đó.
Giải: Dựa vào công thức ta có chu vi hình tam giác đó là:
P = 4 + 8 + 9 = 21 cm.
Cách tính chu vi hình tam giác cân
Tam giác cân là tam giác có 2 cạnh, 2 góc bằng nhau. Đỉnh của tam giác cân là giao điểm của 2 cạnh bên.
Công thức tính chu vi hình tam giác cân: P = 2.a + c
Trong đó:
- a là độ dài hai cạnh bên của tam giác cân
- c là độ dài cạnh đáy của tam giác
Diễn đạt bằng lời: Chu vi tam giác cân bằng 2 lần cạnh bên cộng với cạnh đáy.
Lưu ý: Công thức tính chu vi hình tam giác này cũng được áp dụng để tính chu vi của tam giác vuông cân (tam giác có 1 góc vuông và 2 cạnh bên bằng nhau).
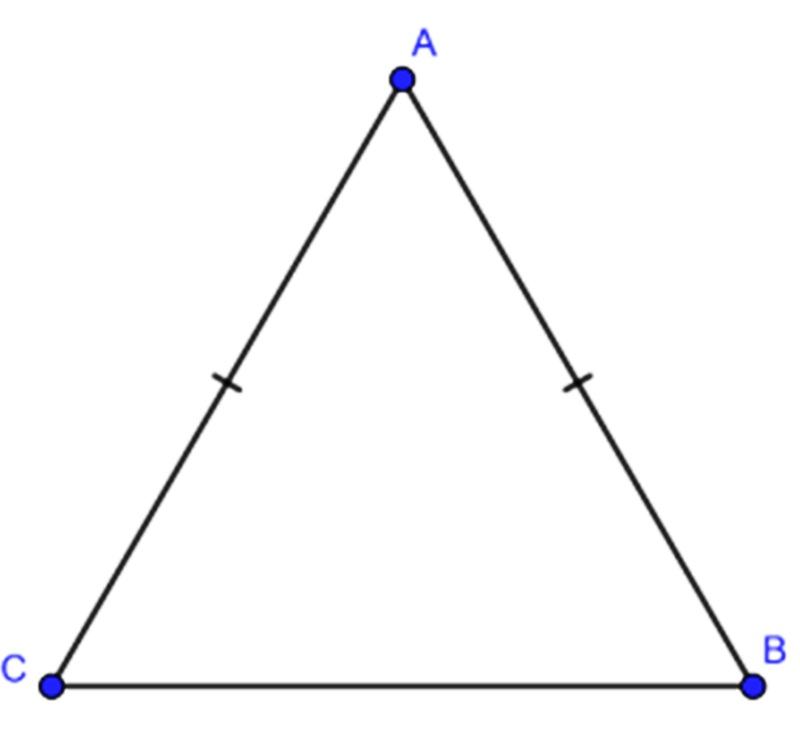
Ví dụ: Tính chu vi tam giác cân ABC khi biết chiều dài cạnh bên là 5 cm, chiều dài cạnh đáy là 8cm.
Giải:
Áp dụng công thức tính chu vi hình tam giác, ta có:
Chu vi tam giác ABC là:
P (ABC) = 2.a + c = (2 x 5) + 8 = 18 (cm).
Cách tính chu vi hình tam giác đều
Tam giác đều là tam giác có 3 cạnh bằng nhau, là trường hợp đặc biệt của tam giác cân.
Công thức tính chu vi hình tam giác đều: P = a + a + a = 3 x a
Trong đó:
- P là chu vi tam giác đều
- a là độ dài cạnh của tam giác
Diễn đạt bằng lời: Chu vi tam giác đều bằng tổng độ dài ba cạnh, mà ba cạnh của tam giác bằng nhau nên tức là bằng độ dài một cạnh nhân ba.
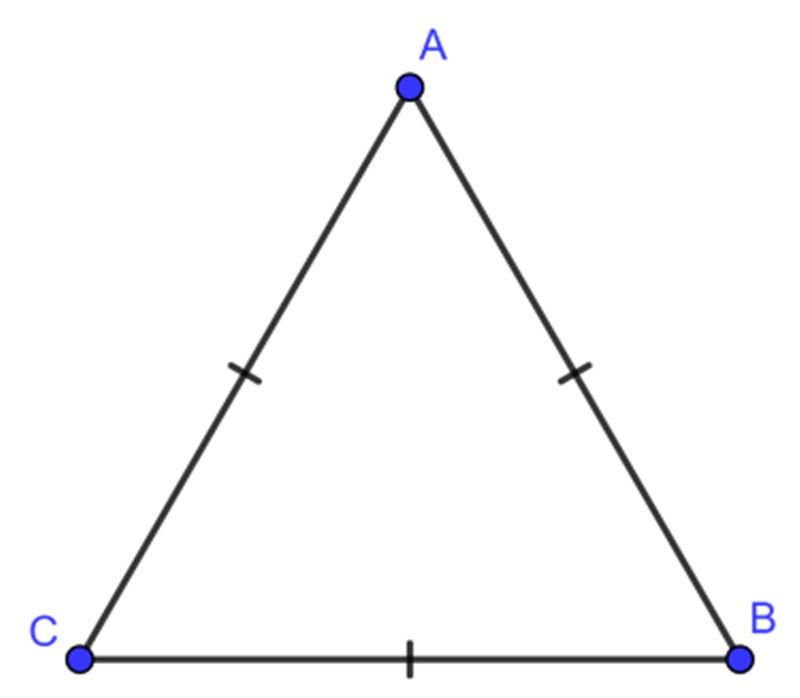
Ví dụ: Tính chu vi tam giác đều ABC với chiều dài cạnh AB = 5 cm.
Vì tam giác ABC là tam giác đều nên ta có, độ dài các cạnh là: AB = AC = BC = 5cm
Dựa vào công thức tính chu vi tam giác đều, ta có:
P (ABC) = 5 x 3 = 15 cm
Cách tính chu vi hình tam giác vuông
Tam giác vuông là tam giác có 1 góc bằng 90°.
Công thức tính chu vi hình tam giác vuông:
P = a + b + c
Trong đó:
- a và b là độ dài hai cạnh của tam giác vuông.
- c là độ dài cạnh huyền của tam giác vuông.
Diễn đạt bằng lời: Chu vi hình tam giác vuông bằng tổng chiều dài 3 cạnh của tam giác.
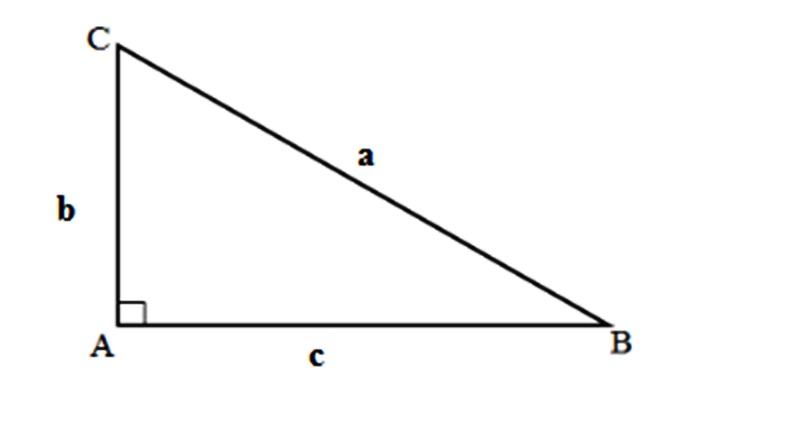
Ví dụ: Cho tam giác vuông ABC với độ dài 3 cạnh lần lượt là 3 cm, 4 cm và 5 cm. Hãy tính chu vi của tam giác vuông.
Giải:
Dựa theo công thức, ta có chu vi tam giác vuông ABC là:
P (ABC) = 3 + 4 + 5 = 12 (cm)
Giải bài tập cách tính chu vi hình tam giác
Sau khi đã tìm hiểu cách tính chu vi hình tam giác, bạn hãy cùng Chúng Tôi giải các bài tập liên quan để nắm vững kiến thức nhé!
Bài tập cách tính chu vi hình tam giác lớp 3
Giải bài 2 trang 174 – SGK Toán lớp 3 tập 1
Tính chu vi hình tam giác có độ dài các cạnh là 35 cm, 26 cm, 40 cm.
Giải:
Chu vi tam giác là:
35 + 26 + 40 = 101(cm)
Đáp số: 101 cm
Giải bài 4 trang 9 – SGK Toán lớp 3 tập 1
Tính chu vi tam giác ABC có kích thước ghi trên hình vẽ:
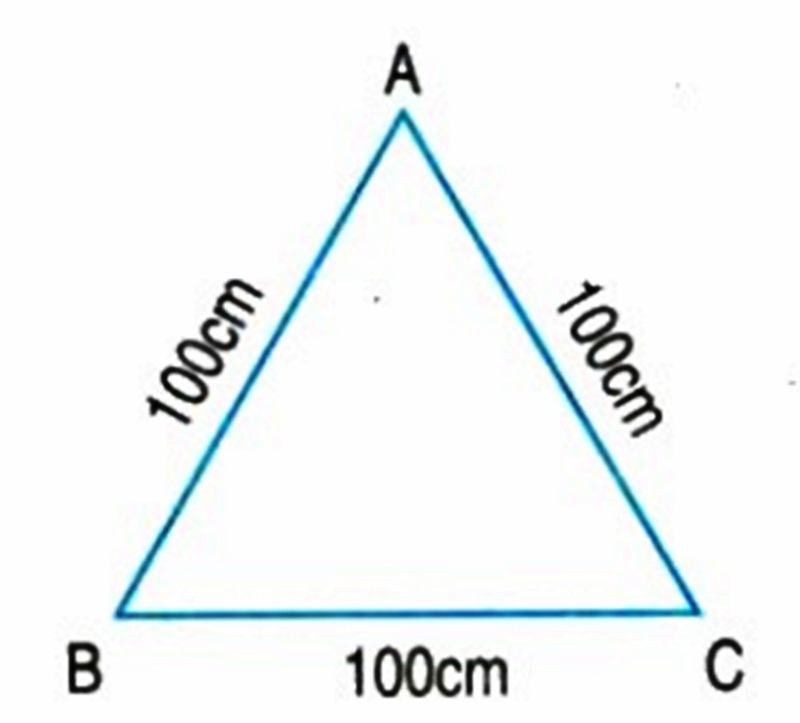
Giải:
Chu vi hình tam giác ABC là:
100 + 100 + 100 = 300 (cm)
Đáp số: 300 cm
Bài tập cách tính chu vi hình tam giác lớp 4
Giải bài 4 trang 44 – SGK Toán lớp 4 tập 1
Độ dài các cạnh của hình tam giác là a, b, c.
a) Gọi P là chu vi của hình tam giác.
Viết công thức tính chu vi P của hình tam giác đó.
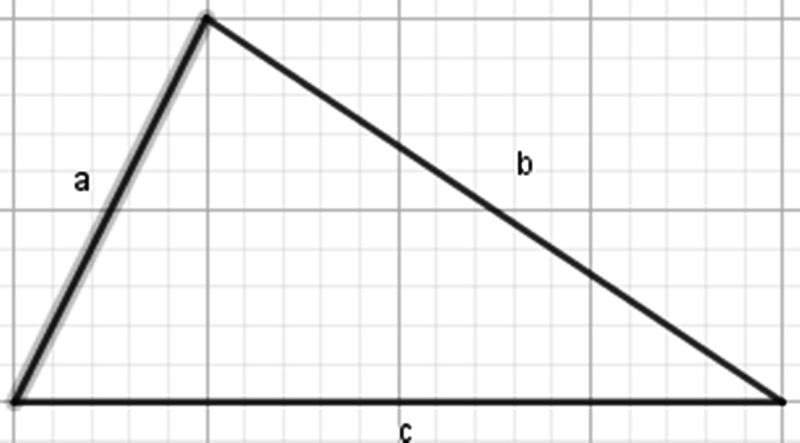
b) Tính chu vi của hình tam giác biết:
a = 5 cm, b = 4 cm và c = 3 cm;
a = 10 cm, b = 10 cm và c = 5 cm;
a = 6 dm, b = 6 dm và c = 6 dm.
Giải:
a) Công thức tính chu vi P của tam giác là :
P = a + b + c.
b) Nếu a = 5cm, b = 4cm và c = 3cm thì P = 5cm + 4cm + 3cm = 12cm.
Nếu a = 10cm, b = 10cm và c = 5cm thì P = 10cm + 10cm + 5cm = 25cm.
Nếu a = 6dm, b = 6dm và c = 6dm thì P = 6dm + 6dm + 6dm = 18dm.

Xem thêm: Tính chất trọng tâm tam giác và cách xác định trọng tâm
Hy vọng bài viết trên của Chúng Tôi đã giúp bạn nắm vững kiến thức về cách tính chu vi hình tam giác. Bạn hãy luyện tập nhiều hơn để làm bài thật tốt nhé. Hẹn gặp lại bạn ở bài viết sau!
Trong chủ đề về cách tính chu vi hình tam giác và giải bài tập trong sách giáo khoa Toán 3, chúng ta đã tìm hiểu về cách tính chu vi của hình tam giác thông qua công thức và giải các bài tập liên quan đến chủ đề này.
Đầu tiên, chúng ta đã nhớ lại định nghĩa hình tam giác, với ba cạnh và ba đỉnh. Chu vi của hình tam giác là tổng độ dài ba cạnh của tam giác. Tiếp theo, chúng ta đã học công thức tính chu vi của tam giác đều và tam giác không đều.
Để tính chu vi của tam giác đều, chúng ta nhân độ dài một cạnh với số đỉnh của tam giác (3). Công thức tổng quát để tính chu vi tam giác đều là: chu vi = 3 x độ dài cạnh. Với các ví dụ trong sách giáo khoa, chúng ta đã áp dụng công thức này để tính chu vi của các tam giác đều với các độ dài cạnh được cho trước.
Đối với tam giác không đều, chúng ta phải tính tổng độ dài của từng cạnh của tam giác. Điều này có nghĩa là chúng ta phải biết độ dài của từng cạnh của tam giác để tính toán chu vi. Trong các bài tập trong sách giáo khoa, chúng ta đã được yêu cầu tính chu vi của các tam giác không đều với các giá trị khác nhau cho từng cạnh.
Qua việc giải các bài tập trong sách giáo khoa Toán 3, chúng ta đã rèn luyện và nắm vững cách tính chu vi hình tam giác. Tư duy toán học của chúng ta cũng được cải thiện qua việc áp dụng công thức và giải quyết các vấn đề liên quan đến hình tam giác và chu vi của nó.
Tóm lại, chủ đề về cách tính chu vi hình tam giác và giải bài tập SGK Toán 3 đã giúp chúng ta hiểu rõ về cách tính chu vi của tam giác đều và tam giác không đều. Qua việc giải quyết các bài tập, chúng ta đã rèn luyện tư duy toán học và nắm vững các kiến thức cơ bản về hình học và tính toán trong môn Toán.
Cảm ơn bạn đã xem bài viết Cách tính chu vi hình tam giác – Giải bài tập SGK Toán 3 tại Thcslytutrongst.edu.vn bạn có thể bình luận, xem thêm các bài viết liên quan ở phía dưới và mong rằng sẽ giúp ích cho bạn những thông tin thú vị.
Từ Khoá Liên Quan:
1. Tam giác
2. Chu vi
3. Cách tính
4. Hình tam giác
5. Bài tập
6. SGK Toán 3
7. Độ dài
8. Tam giác đều
9. Tam giác vuông
10. Tam giác cân
11. Đường cao
12. Tử bình
13. Biện luận
14. Phân tích
15. Thực hành


