Bạn đang xem bài viết Tính chất dãy tỉ số bằng nhau? 6 dạng bài tập phổ biến tại Thcslytutrongst.edu.vn bạn có thể truy cập nhanh thông tin cần thiết tại phần mục lục bài viết phía dưới.
Dãy tỉ số bằng nhau là một khái niệm quan trọng trong toán học, được áp dụng rộng rãi trong các bài toán thuộc lĩnh vực đại số và hình học. Tính chất này cho phép ta dễ dàng rút ra các kết luận quan trọng về sự tương đồng giữa các phần tử trong một dãy số.
Trong bài viết này, chúng ta sẽ tìm hiểu về các tính chất cơ bản của dãy tỉ số bằng nhau và áp dụng chúng vào giải các bài tập phổ biến. Cụ thể, chúng ta sẽ tập trung vào 6 dạng bài tập thường gặp liên quan đến tính chất này.
Dạng bài tập thứ nhất là về việc tìm số lượng phần tử trong một dãy tỉ số bằng nhau, khi biết số lượng phần tử đã cho và tổng của chúng. Chúng ta sẽ tìm hiểu cách sử dụng phép tính trung bình để giải quyết bài toán này.
Dạng bài tập thứ hai là về việc tìm giá trị của một phần tử trong dãy tỉ số bằng nhau, khi biết giá trị của các phần tử khác trong dãy. Chúng ta sẽ khám phá cách sử dụng quy tắc nhân và chia để tìm giá trị cần tìm.
Dạng bài tập thứ ba là về việc xác định tính chất của dãy tỉ số bằng nhau, dựa trên các thông tin về giá trị và vị trí của các phần tử trong dãy. Chúng ta sẽ sử dụng phép đổi vị trí để phân tích các khái niệm này.
Dạng bài tập thứ tư là về việc xác định tổng số phần tử trong dãy tỉ số bằng nhau, biết tổng của các phần tử và tỉ số giữa chúng. Chúng ta sẽ sử dụng phương pháp giải đồng nhất để giải quyết vấn đề này.
Dạng bài tập thứ năm là về việc xác định tổng các phần tử trong dãy tỉ số bằng nhau, khi biết giá trị của các phần tử và tỉ số giữa chúng. Chúng ta sẽ kết hợp các quy tắc cộng và nhân để giải quyết bài toán này.
Cuối cùng, dạng bài tập thứ sáu là về việc xác định tổng của các bình phương hoặc các lũy thừa khác của các phần tử trong dãy tỉ số bằng nhau. Chúng ta sẽ sử dụng các quy tắc rút gọn để đơn giản hóa các bài toán này.
Với 6 dạng bài tập trên, chúng ta sẽ có được một cái nhìn tổng quan về tính chất của dãy tỉ số bằng nhau và áp dụng chúng vào các bài toán cụ thể. Hi vọng rằng bài viết này sẽ giúp bạn hiểu rõ hơn và áp dụng thành thạo các kiến thức về tính chất này trong thực tế.
Chuyên đề tính chất dãy tỉ số bằng nhau là một bài học quan trọng nằm trong chương trình toán lớp 7. Tuy nhiên không phải bạn học sinh nào cũng nắm vững kiến thức này. Tính chất dãy tỉ số bằng nhau là gì? Chúng Tôi sẽ cùng bạn hệ thống lại kiến thức và ôn tập kĩ hơn nhé!
Định nghĩa, tính chất của tỉ lệ thức
Định nghĩa tỉ lệ thức
Tỉ lệ thức là đẳng thức của hai tỉ số 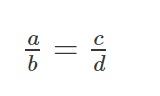
Tỷ lệ thức 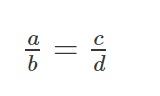 còn được viết dưới dạng: a:b = c:d
còn được viết dưới dạng: a:b = c:d
Trong đó:
- a, b, c, d là các số hạng của tỉ lệ thức.
- a và d là các số hạng ngoài hay ngoại tỉ.
- b và d là các số hạng trong hay trung tỉ.
Tính chất tỉ lệ thức
Tính chất 1 (Tính chất cơ bản)
Nếu 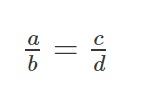 thì a.d = b.c
thì a.d = b.c
Tính chất 2 (Tính chất hoán vị)
Nếu a.d = b.c và a, b, c, d khác 0 thì ta có có tỉ lệ thức:
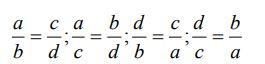
Chủ đề liên quan:
- Tính chất cơ bản của phân thức là gì? 3 Dạng toán cơ bản của phân thức
Tính chất dãy tỉ số bằng nhau
Tính chất dãy tỉ số bằng nhau

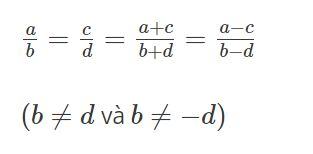
Tính chất trên còn được mở rộng cho dãy tỉ số bằng nhau:
Chẳng hạn:
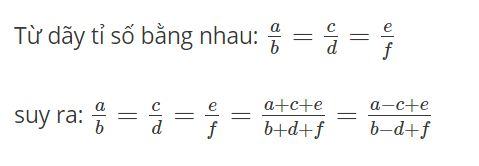
(Giả thiết các tỉ số đều có nghĩa).

Nội dung mở rộng liên quan đến tính chất dãy tỉ số bằng nhau
Liên quan đến tinh chất dãy tỉ số bằng nhau, ta có nội dung mở rộng như sau:
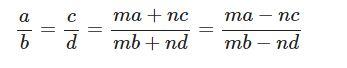
Chú ý:
Khi nói các số x, y, z tỉ lệ với các số a, b, c tức là ta có:

Ví dụ: Tìm x, y biết:
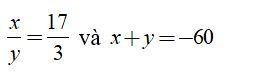
Hướng dẫn giải:
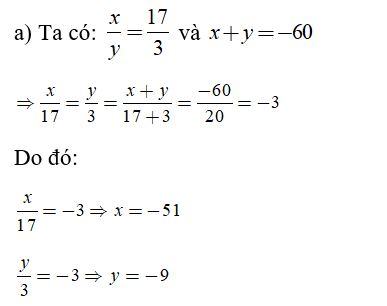
Các dạng bài tập tính chất dãy tỉ số bằng nhau
Dạng 1: Tìm hai số x; y biết tổng (hoặc hiệu) và tỉ số của chúng
Phương pháp giải dạng 1:
Để tìm hai số x;y khi biết tổng x + y = s và tỉ số 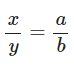 ta làm như sau:
ta làm như sau:
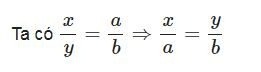
Áp dụng dãy tỉ số bằng nhau ta được:
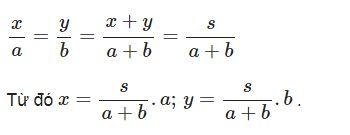
Để tìm hai số x; y khi biết hiệu x − y = p và tỉ số 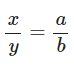 ta làm như sau:
ta làm như sau:
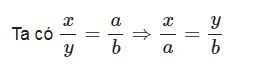
Áp dụng dãy tỉ số bằng nhau ta được:
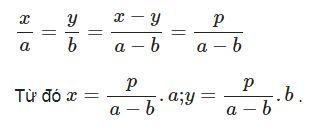
Ví dụ 1:
Tìm hai số x và y, biết: ![]() và x + y = 20
và x + y = 20
Lời giải:
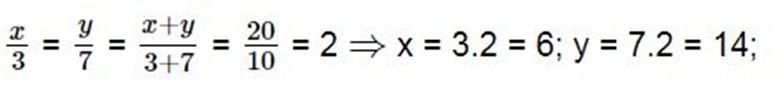
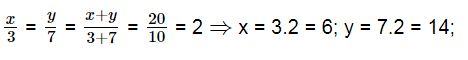
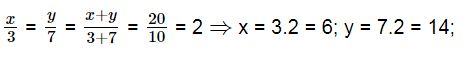
Ví dụ 2: Số học sinh bốn khối 6, 7, 8, 9 tỉ lệ với các số 9, 8, 7, 6. Biết rằng số học sinh khối 9 ít hơn số học sinh khối 7 là 70 học sinh. Tìm số học sinh mỗi khối.
Lời giải:
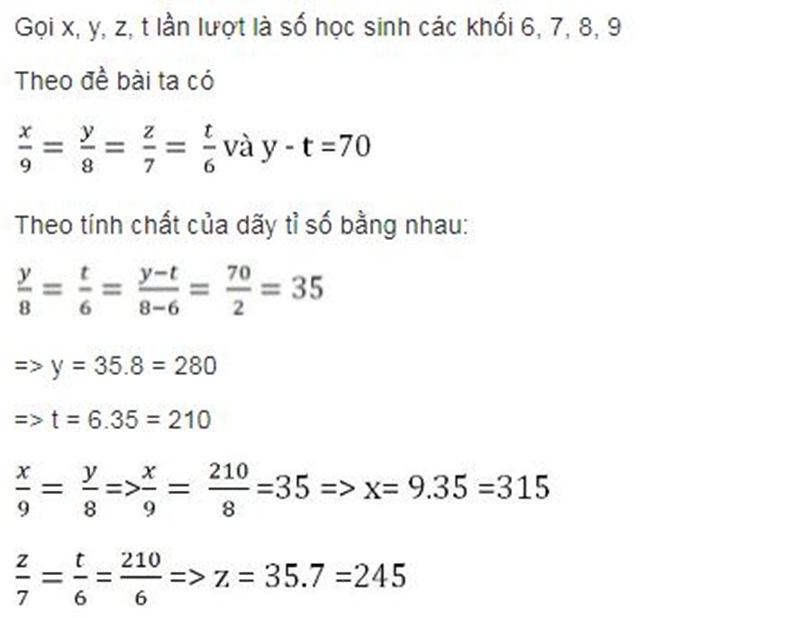
Dạng 2: Chia một số thành các phần tỉ lệ với các số cho trước
Phương pháp giải dạng 2:
Giả sử chia số P thành ba phần x, y, z tỉ lệ với các số a, b, c ta làm như sau:
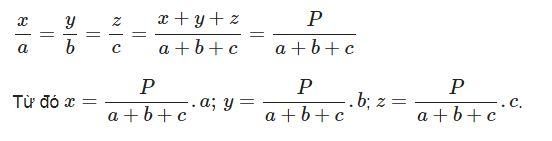
Ví dụ 1:
Trường Trung học cơ sở Nguyễn Huệ có bốn khối 6, 7, 8, 9 và tổng số học sinh toàn trường là 660 em. Tính số học sinh của mỗi khối lớp, biết rằng số học sinh khối 6, 7, 8, 9 theo thứ tự tỉ lệ với các số 3; 3,5; 4,5; 4.
Lời giải:
Gọi số học sinh của các khối lớp 6, 7, 8, 9 lần lượt là x, y, z, t (em).
Vì tổng số học sinh của trường là 660 em nên ta có x + y + z + t = 660.
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
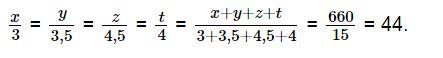
Từ đó, ta có:
x = 44.3 = 132; y = 44.3,5 = 154; z = 44.4,5 = 198; t = 44.4 = 176.
Vậy số học sinh của các khối 6, 7, 8, 9 lần lượt là 132, 154, 198, 176 em.
Ví dụ 2:
Ba học sinh A, B, C có số điểm mười tỉ lệ với các số 2, 3, 4. Biết rằng tổng số điểm mười của A và C lớn hơn B là 6 điểm mười. Hỏi mỗi em có bao nhiêu điểm 10?
Lời giải:
Gọi a, b, c lần lượt là số điểm 10 của ba học sinh A, B, C.
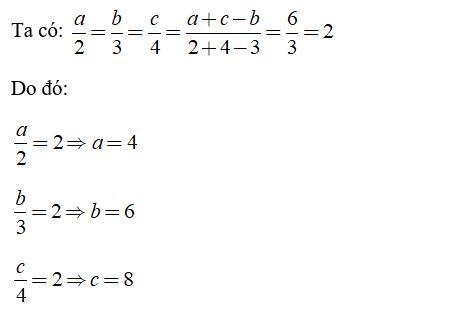
Vậy bạn A có 4 điểm 10; bạn B có 6 điểm 10; bạn C có 8 điểm 10.
Dạng 3: Tìm hai số biết tích và tỉ số của chúng
Phương pháp giải dạng 3:
Tìm hai số x; y biết x. y = P và 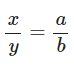
Ở dạng này, ta có 2 cách làm như sau:
Cách 1:
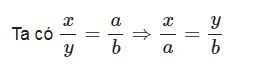
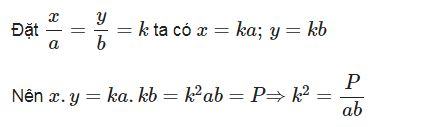
Từ đó tìm được k sau đó tìm được x,y
Cách 2:

Ví dụ: Tìm x, y biết: 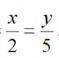 và x.y = 10
và x.y = 10
Lời giải:
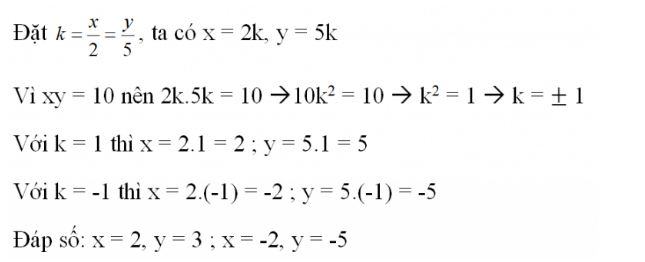
Dạng 4: Chứng minh đẳng thức từ một tỉ lệ thức cho trước
Phương pháp giải dạng 4:
Áp dụng tính chất tỉ lệ thức và tính chất dãy tỉ số bằng nhau.
Ví dụ:
Chứng minh rằng từ tỉ lệ thức 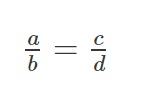 (a ≠ b; c ≠ d), ta có thể suy ra tỉ lệ thức
(a ≠ b; c ≠ d), ta có thể suy ra tỉ lệ thức 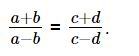
Lời giải:
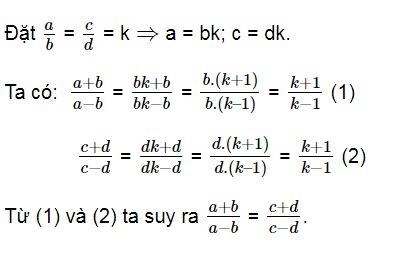
Dạng 5: Thay tỉ số giữa các số hữu tỉ bằng tỉ số giữa các số nguyên
Phương pháp giải dạng 5:
- Viết các số hữu tỉ dưới dạng phân số.
- Thực hiện phép chia phân số.
Ví dụ: Thay tỉ số giữa các số hữu tỉ bằng tỉ số giữa các số nguyên:

Lời giải:
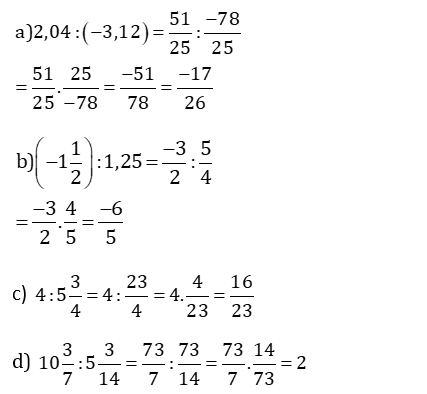
Dạng 6: Tìm số hạng chưa biết trong một tỉ lệ thức
Phương pháp giải dạng 6:
Trong một tỉ lệ thức, ta có thể tìm một số hạng chưa biết khi biết ba số hạng kia.
Ví dụ: Tìm x trong tỉ lệ thức sau:
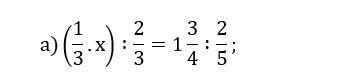
Lời giải:
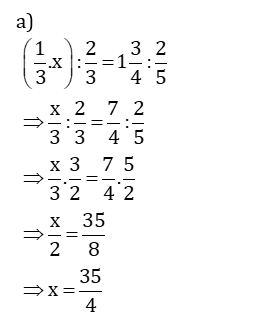
Các bài tập về tính chất dãy tỉ số bằng nhau
Với những dạng bài tập về tính chất dãy tỉ số bằng nhau kèm theo ví dụ mà Chúng Tôi đã hệ thống như trên, các bạn hãy luyện tập thông qua những bài tập dưới đây nhé!
Bài 1: Tìm hai số x, y biết: 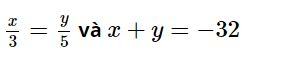
Lời giải:
Áp dụng dãy tỉ số bằng nhau ta có:
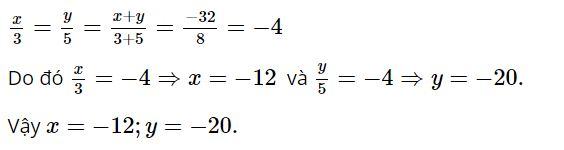
Bài 2: Tìm hai số x, y biết: 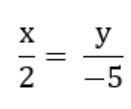 và x − y = −7
và x − y = −7
Lời giải:
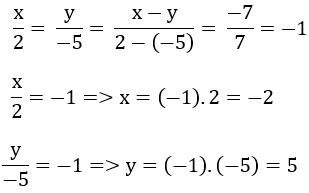
Bài 3: Số viên bi của ba bạn Minh, Hùng, Dũng tỉ lệ với các số 2; 4; 5. Tính số viên bi của mỗi bạn biết rằng ba bạn có 44 viên bi.
Lời giải:

Bài 4: Hai lớp 7A và 7B đi lao động trồng cây. Biết rằng tỉ số giữa số cây trồng được của lớp 7A là 0,8 và lớp 7B trồng nhiều hơn 20 cây. Tính số cây mỗi lớp đã trồng.
Lời giải:
Gọi x, y lần lượt là số cây trồng được của lớp 7A, 7B (0 < x < 20, 20 < y; x, y ∈ N*).
Theo đề bài ta có:
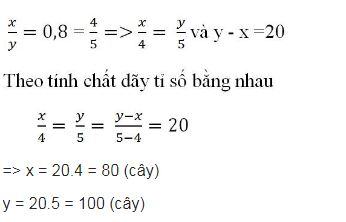
Bài 5: Tìm x, y biết: 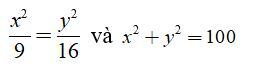
Lời giải:
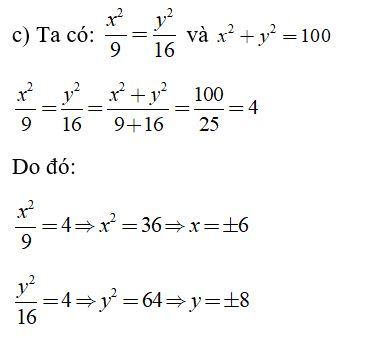
Bài 6: Chứng minh rằng nếu  thì:
thì:
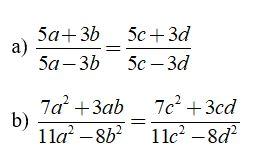
Lời giải:
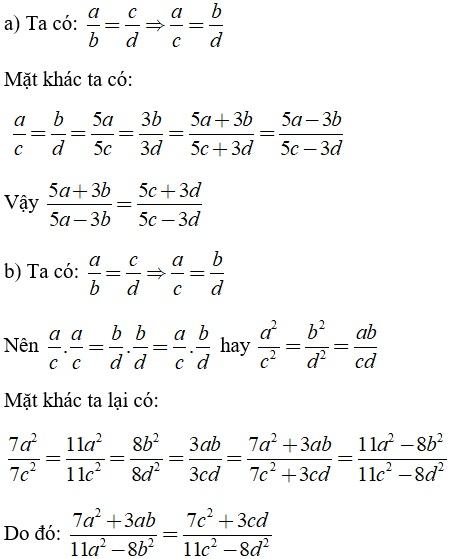
Bài viết trên của Chúng Tôi đã chia sẻ đến bạn chủ đề tính chất dãy tỉ số bằng nhau và 6 dạng bài tập cơ bản liên quan đến bài toán này. Chúc các bạn học tập tốt. Hẹn gặp lại ở bài viết sau!
Tham khảo thêm về kiến thức hình học:
- Tính chất đường trung trực của một đoạn thẳng? Top 10 bài tập vận dụng
- Tính chất trọng tâm tam giác và cách xác định trọng tâm
- Tính chất đường trung trực là gì? Tổng hợp đủ các tính chất
Tính chất dãy tỉ số bằng nhau là một khái niệm quan trọng trong toán học, đặc biệt trong lĩnh vực số học. Để hiểu rõ hơn về tính chất này, chúng ta cần xem xét các dạng bài tập phổ biến liên quan đến dãy tỉ số bằng nhau.
Đầu tiên, một dạng bài tập phổ biến liên quan đến tính chất này là tìm tổng các số trong một dãy tỉ số bằng nhau. Đây là bài toán đòi hỏi chúng ta phải tìm hiểu cách tính tổng một dãy số học hình thành từ các tỉ số bằng nhau. Điều này thường liên quan đến việc sử dụng công thức tính tổng các phần tử trong dãy.
Tiếp theo, một dạng bài tập khác liên quan đến tính chất dãy tỉ số bằng nhau là xác định số phần tử trong dãy. Với thông tin về tổng và tỉ số bằng nhau, chúng ta có thể tìm ra số phần tử cần tìm trong dãy này. Đây là một bài toán tương đối phức tạp và thường đòi hỏi chúng ta áp dụng các công thức và phương pháp trong lĩnh vực tam giác số học để giải quyết.
Bên cạnh đó, một loại bài tập khác liên quan đến tính chất dãy tỉ số bằng nhau là xác định giá trị của các phần tử trong dãy. Đây là một bài toán thú vị và thường đòi hỏi chúng ta phải áp dụng các công thức tính giá trị của phần tử trong một dãy số học hình thành từ các tỉ số bằng nhau.
Ngoài ra, chúng ta có thể gặp phải các bài tập với tính chất dãy tỉ số bằng nhau cùng với các ràng buộc. Ví dụ, đề bài có thể yêu cầu ta tìm cách sắp xếp các phần tử trong dãy để thỏa mãn tính chất tỉ số bằng nhau và các điều kiện khác như sắp xếp tăng dần hay giảm dần, điều kiện đặc biệt về vị trí của các phần tử trong dãy, v.v. Điều này đòi hỏi chúng ta phải áp dụng các kiến thức về các phương pháp và quy tắc sắp xếp dãy số.
Cuối cùng, một dạng bài tập cuối cùng liên quan đến tính chất dãy tỉ số bằng nhau là phân tích các phần tử trong dãy. Đây là một bài toán phân tích dãy nổi bật và thường đòi hỏi chúng ta phải áp dụng kiến thức về tỉ số bằng nhau và các công thức phân tích/phân rã dãy số.
Từ các dạng bài tập trên, chúng ta có thể thấy rằng tính chất dãy tỉ số bằng nhau có những ứng dụng rất đa dạng trong toán học. Việc nắm vững các kiến thức và kỹ năng liên quan đến tính chất này không chỉ giúp chúng ta giải quyết các bài tập mà còn là nền tảng quan trọng để khám phá và phát triển những kiến thức mới trong lĩnh vực toán học.
Cảm ơn bạn đã xem bài viết Tính chất dãy tỉ số bằng nhau? 6 dạng bài tập phổ biến tại Thcslytutrongst.edu.vn bạn có thể bình luận, xem thêm các bài viết liên quan ở phía dưới và mong rằng sẽ giúp ích cho bạn những thông tin thú vị.
Từ Khoá Liên Quan:
1. Dãy tỉ số bằng nhau
2. Tính chất của dãy tỉ số bằng nhau
3. Dãy tỉ số bằng nhau trong toán học
4. Bài tập về tính chất của dãy tỉ số bằng nhau
5. Các bài tập liên quan đến dãy tỉ số bằng nhau
6. Định lí về dãy tỉ số bằng nhau
7. Dãy tỉ số cấp số cộng
8. Tính chất của dãy tỉ số cấp số cộng
9. Bài tập về dãy tỉ số cấp số cộng
10. Dãy tỉ số cấp số nhân
11. Tính chất của dãy tỉ số cấp số nhân
12. Bài tập về dãy tỉ số cấp số nhân
13. Dãy tỉ số Fibonacci và tính chất của nó
14. Bài tập về dãy tỉ số Fibonacci
15. Ứng dụng của dãy tỉ số bằng nhau trong thực tế


