Bạn đang xem bài viết Tính chất cơ bản của phân thức là gì? 3 Dạng toán cơ bản của phân thức tại Thcslytutrongst.edu.vn bạn có thể truy cập nhanh thông tin cần thiết tại phần mục lục bài viết phía dưới.
Phân thức là một khái niệm quan trọng trong toán học, được sử dụng để biểu diễn tỉ lệ giữa hai đại lượng. Tính chất cơ bản của phân thức phản ánh các quy tắc căn bản trong việc thực hiện các phép tính, rút gọn và thực hiện các phép biến đổi trên các phân thức.
Có ba dạng toán cơ bản của phân thức: cộng, trừ, nhân, chia. Cộng và trừ phân thức được thực hiện bằng cách tìm chung mẫu số rồi thực hiện phép tính với tử số. Đối với phép nhân, ta nhân tử số và mẫu số của các phân thức với nhau. Phép chia cũng tương tự, chỉ cần lấy phân thức thứ nhất nhân với nghịch đảo của phân thức thứ hai.
Việc nắm vững các dạng toán cơ bản này giúp chúng ta dễ dàng thực hiện các phép tính và biến đổi trên phân thức một cách chính xác và nhanh chóng. Ngoài ra, cũng cần lưu ý một số quy tắc cần tuân thủ khi làm việc với phân thức, bao gồm việc không chia cho 0 và rút gọn phân thức về dạng tối giản.
Tóm lại, tính chất cơ bản của phân thức là các quy tắc để thực hiện các phép tính cộng, trừ, nhân và chia trên phân thức. Việc hiểu và áp dụng đúng các quy tắc này sẽ giúp chúng ta giai đoạn khái niệm phân thức trong toán học một cách hiệu quả.
Toán học là môn học rất được chú trọng trong công tác giảng dạy. Hôm nay, Chúng Tôi sẽ giới thiệu đến các bạn tính chất cơ bản của phân thức trong đại số. Chúng ta cùng tìm hiểu nhé!
Tính chất cơ bản của phân thức
Nếu nhân cả tử và mẫu của một phân thức với cùng một đa thức khác đa thức không thì được một phân thức bằng phân thức đã cho.

Nếu chia cả tử và mẫu của một phân thức với cùng một đa thức khác đa thức không thì được một phân thức bằng phân thức đã cho.
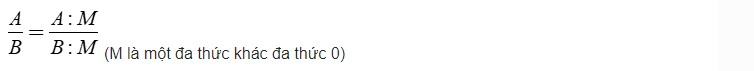

Quy tắc đổi dấu
Nếu đổi dấu cả tử và mẫu của một phân thức ta sẽ được một phân thức mới bằng với phân thức đã cho: A/B = -A/-B
- Đổi dấu phân thức và tử số: A/B = -(-A)/B.
- Đổi dấu phân thức và mẫu số: A/B = -(A)/-B.
- Đổi dấu mẫu: A/-B = -(A)/B.
Khi bỏ dấu ngoặc có dấu “−” đứng trước, ta phải đối dấu tất cả các số hạng trong dấu ngoặc dấu “−” thành dấu “+” và dấu “+” thành dấu “−”. Khi bỏ dấu ngoặc có dấu “+” đứng trước thì dấu các số hạng trong ngoặc vẫn giữ nguyên.
Chủ đề liên quan:
- Tính chất dãy tỉ số bằng nhau? 6 dạng bài tập phổ biến
Bài tập về tính chất cơ bản của phân thức
Toán 8 tính chất cơ bản của phân thức được áp dụng với đa dạng các bài tập từ cơ bản đến nâng cao và vẫn còn sử dụng thường xuyên khi lên các lớp trên.
Dạng bài quy đồng mẫu thức
Bước 1: Tìm mẫu chung
- Phân tích phần hệ số thành thừa số nguyên tố và phần biến nhân tử.
- Mẫu chung bao gồm: phận hệ số của các hệ số mẫu và phần biến là tích các nhân tử chung và riêng của mỗi phần tử lấy số mũ lớn nhất.
Bước 2: Tìm nhân tử phụ của mỗi phân thức bằng cách lấy mẫu chung chia cho từng mẫu đa phân tích thành phân tử ở bước 1.
Bước 3: Nhân cả tử và mẫu của mỗi phân thức với nhân tử phụ tương ứng.
Dạng bài rút gọn phân thức đại số
Dạng bài rút gọn phân thức đại số là dạng bài đơn giản tuy nhiên cần khả năng phân tích tốt để có thể tìm ra cách giải nhanh nhất. Đây là cách biến đổi những phân thức phức tạp thành những phân thức đơn giản hơn và bằng với phân thức đa cho.
Muốn rút gọn phân thức một cách nhanh chóng ta có thể làm như sau:
- Phân tích tử và mẫu thành nhân tử để có thể tìm được nhân tử chung.
- Chia cả tử và mẫu cho nhân tử chung để rút gọn biểu thức.
Ví dụ: Rút gọn phân thức sau A =(x + 2×2)/( x2 – x)
Bước 1: Phân tích tử và mẫu để tìm nhân tử chung
A = x(1 + 2x)/x(x – 1)
Vậy ta có nhân tử chung là x.
Bước 2: Chia cả tử và mẫu cho nhân tử chung x
Vậy ta được phân thức rút gọn b = (1 + 2x)/(x – 1) bằng với phân thức A = (x + 2x)/(x2 – x).
Dạng bài biến đổi các biểu thức hữu tỉ
Sử dụng các quy tắc cộng, trừ, nhân, chia phân thức để biến đổi các biến đổi các biểu thức hữu tỉ thành phân thức.
Bài 4 trang 38 SGK Toán 8 Tập 1
Cô giáo yêu cầu mỗi bạn cho một ví dụ về hai phân thức bằng nhau. Dưới đây là những ví dụ mà các bạn Lan, Hùng, Giang, Huy đã cho:

Em hãy dùng tính chất cơ bản của phân thức và qui tắc đổi dấu để giải thích ai viết đúng, ai viết sai. Nếu có chỗ nào sai em hãy sửa lại cho đúng.
Hướng dẫn giải:
Áp dụng tính chất cơ bản của phân thức, ta thấy:
Lan viết đúng, vì:

(Nhân cả tử và mẫu với x)
Hùng viết sai vì:

Bài 5 trang 38 SGK Toán 8 Tập 1
Dựa theo tính chất cơ bản của phân thức. Hãy điền đa thức thích hợp vào mỗi chỗ trống trong các đa thức sau:
Hướng dẫn giải:
Áp dụng các tính chất cơ bản của phân thức ta có :
a) Từ (x – 1)(x + 1) để có được x – 1 ta cần chia cho x + 1
Vậy ta chia cả tử và mẫu của phân thức thứ nhất cho x + 1:
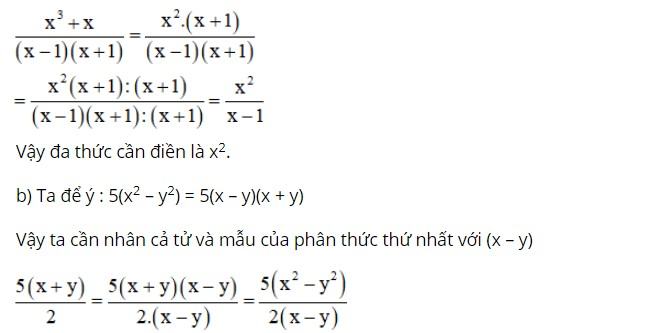
Vậy đa thức cần điền là 2(x – y).

Trên đây là tính chất cơ bản của phân thức và một số dạng bài đặc trưng của phân thức đại số lớp 8 mà Chúng Tôi muốn giới thiệu đến các bạn. Với hy vọng giúp các bạn hiểu rõ hơn về dạng bài tập này. Đừng quên theo dõi Chúng Tôi để cập nhật thông tin mới mỗi ngày nhé!
Có thể bạn quan tâm:
- Tính chất đường phân giác trong tam giác?
- Tính chất hình thang vuông? Bài tập về hình thang vuông
Tính chất cơ bản của phân thức:
Phân thức là một biểu thức số học có dạng a/b, trong đó a và b là các biểu thức đại số và b khác không. Tính chất cơ bản của phân thức đó là:
1. Tính chất phân thức: Phân thức có thể được rút gọn bằng cách tối giản hóa a và b đồng thời hay tìm các ước chung lớn nhất của a và b, sau đó chia cả hai phần tử cho ước chung lớn nhất đó để thu được phân thức tối giản.
2. Tính chất tổng, hiệu, tích và thương phân thức: Phân thức cũng tuân theo các quy tắc cộng, trừ, nhân và chia từng phần tử trong biểu thức phân thức. Điều này có nghĩa là khi thực hiện các phép toán này, ta chỉ cần thực hiện các phép toán tương ứng trên từng phần tử trong phân thức.
3. Tính chất đảo ngược: Nếu hai phân thức a/b và c/d bằng nhau, thì có thể nói a/b = c/d và ngược lại. Điều này có nghĩa là nếu hai phân thức có cùng giá trị số, thì các tử số và mẫu số tương ứng của chúng cũng phải bằng nhau.
Các dạng toán cơ bản của phân thức:
1. Rút gọn phân thức: Bước đầu thường là rút gọn phân thức để thay thế cho phân thức ban đầu bằng phân thức tối giản hơn. Điều này giúp ta thực hiện các phép toán và giải quyết các bài toán liên quan đến phân thức một cách dễ dàng.
2. Cộng, trừ, nhân và chia phân thức: Như đã đề cập trong tính chất thứ hai, các phép toán này được thực hiện bằng cách thực hiện các phép toán tương ứng trên từng phần tử trong phân thức. Việc này có thể được thực hiện bằng cách tìm ước chung lớn nhất và các quy tắc cộng, trừ, nhân, chia đối với phân thức.
3. Giải phương trình phân thức: Một dạng phân thức có thể xuất hiện trong các phương trình và việc giải phương trình đòi hỏi ta phải thực hiện các phép toán và rút gọn phân thức tìm nghiệm của phương trình. Đây là một ứng dụng cơ bản của phân thức trong việc giải quyết các bài toán đại số.
Cảm ơn bạn đã xem bài viết Tính chất cơ bản của phân thức là gì? 3 Dạng toán cơ bản của phân thức tại Thcslytutrongst.edu.vn bạn có thể bình luận, xem thêm các bài viết liên quan ở phía dưới và mong rằng sẽ giúp ích cho bạn những thông tin thú vị.
Từ Khoá Liên Quan:
1. Phân thức
2. Tính chất cơ bản
3. Đồng dạng phân thức
4. Rút gọn phân thức
5. Tìm giá trị của phân thức
6. Phân thức tối giản
7. Bài toán phân thức
8. Phân thức đơn giản
9. Tổng, hiệu, tích, thương phân thức
10. Đối xứng phân thức
11. Định lí về phân thức
12. Phân thức không đơn giản
13. Phân thức bất quy tắc
14. Phân thức bậc hai
15. Bài toán về phân thức.


