Bạn đang xem bài viết Hawngf ddawngr thuwcs – Bài tập về 7 hằng đẳng thức đáng nhớ tại Thcslytutrongst.edu.vn bạn có thể truy cập nhanh thông tin cần thiết tại phần mục lục bài viết phía dưới.
Hàng đẳng thức là một phần quan trọng trong toán học, đóng vai trò quan trọng trong việc giải quyết các bài toán và tìm ra những kết quả chính xác. Trong số các hàng đẳng thức, có một nhóm đặc biệt mà các học sinh thường hay gặp và phải ghi nhớ, đó là 7 hằng đẳng thức đáng nhớ trong hình học và toán học. Những hằng đẳng thức này không chỉ giúp các học sinh hiểu sâu về các khái niệm toán học mà còn giúp các em dễ dàng áp dụng vào các bài toán thực tế.
HĐT (hằng đẳng thức) gồm 7 đẳng thức cơ bản nhất mà mỗi người học Toán cần phải nắm vững. Vậy có những hằng đẳng thức (hawngf ddawngr thuwcs) nào? Mời bạn tham khảo nội dung bài viết này của Chúng Tôi nhé.
7 hằng đẳng thức đáng nhớ (hawngf ddawngr thuwcs)
Bình phương của một tổng
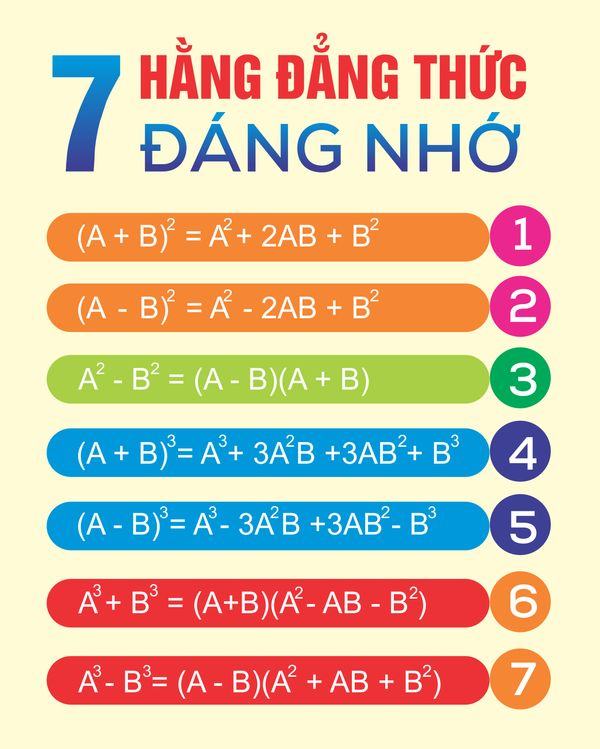
Đằng thức: (a + b)2 = a2 + 2 * a * b + b2
Diễn giải: Bình phương của một tổng bằng bình phương số thứ nhất, cộng với hai lần tích số thứ nhất và số thứ hai, cộng với bình phương số thứ hai.
Bình phương của một hiệu
Đẳng thức: (a – b)2 = a2 – 2 * a * b + b2
Diễn giải: Bình phương của một hiệu bằng bình phương số thứ nhất, trừ đi hai lần tích số thứ nhất và số thứ hai, cộng với bình phương số thứ hai.
Hiệu hai bình phương
Đẳng thức: a2 – b2 = (a – b) * (a + b)
Diễn giải: Hiệu hai bình phương bằng hiệu của số thứ nhất và số thứ hai nhân với tổng của số thứ nhất và số thứ hai.
Lập phương của một tổng
Đẳng thức: (a + b)3 = a3 + 3 * a2 * b + 3 * a * b2 + b3
Diễn giải: Lập phương của một tổng bằng lập phương của số thứ nhất, cộng ba lần tích bình phương của số thứ nhất với số thứ hai, cộng ba lần tích số thứ nhất với bình phương của số thứ hai, cộng lập phương của số thứ hai.
Đây là một dạng của hằng đẳng thức bậc 3.
Lập phương của một hiệu
Đẳng thức: (a – b)3 = a3 – 3 * a2 * b + 3 * a * b2 – b3
Diễn giải: Lập phương của một hiệu bằng lập phương của số thứ nhất trừ đi ba lần tích của bình phương số thứ nhất nhân cho số thứ hai, cộng với ba lần tích của số thứ nhất nhân với bình phương của số thứ hai, rồi sau đó trừ đi lập phương của số thứ hai.
Tổng hai lập phương
Đẳng thức: a3 + b3 = (a + b) * (a2 – a * b + b2)
Diễn giải: Tổng hai lập phương bằng tổng của số thứ nhất và số thứ hai Nhân với bình phương thiếu của hiệu.
Hiệu hai lập phương
Đẳng thức: a3 – b3 = (a – b) * (a2 + a * b + b2)
Diễn giải: Hiệu hai lập phương bằng hiệu của số thứ nhất và số thứ hai nhân với bình phương thiếu của tổng.
Cách ghi nhớ bảy hằng đẳng thức đáng nhớ hiệu quả
Dưới đây là 3 cách ghi nhớ bảy hằng đẳng thức (hawngf ddawngr thuwcs) đáng nhớ lớp 9 hiệu quả nhất mà Chúng Tôi dành cho bạn:
Luyện tập thường xuyên
Học đi đôi với hành. Việc luyện tập thường xuyên sẽ giúp bạn ghi nhớ và vận dụng nhuần nhuyễn hơn bảy hằng đẳng thức (hawngf ddawngr thuwcs).
Bạn có thể thiết kế các bài tập ở nhiều dạng như điền vào chỗ chấm, cho sẵn một vế, viết vế còn lại.
Viết vào giấy note
Bạn có thể viết 7 hằng đẳng thức vào những tờ giấy ghi nhớ nhỏ, nhiều màu sắc như cách học từ vựng Tiếng Anh rồi dán lên góc học tập.
Học bài qua bài hát
Đọc bằng lời những hằng đẳng thức có thể khó nhớ nhưng đưa chúng vào trong bài hát thì việc ghi nhớ sẽ dễ dàng hơn.
Hiện nay có bài chế “Sau tất cả” với nội dung là 7 hằng đẳng thức. Giai điệu dễ nghe này đã thu hút sự chú ý của rất nhiều bạn trẻ.
Nhờ đó việc ghi nhớ bảy hằng đẳng thức không còn khô khan mà trở nên thuận lợi hơn.

Bài tập về 7 hằng đẳng thức đáng nhớ
Để củng cố nội dung 7 hằng đẳng thức đáng nhớ (hawngf ddawngr thuwcs), chúng ta cùng giải những bài tập trong SGK Toán nhé.
Câu hỏi trang 9 SGK Toán 8 tập 1
Với a và b là hai số bất kỳ, thực hiện phép tính (a + b) * (a + b).
Hướng dẫn giải
(a + b) * (a + b) = a * (a + b) + b * (a + b)
= a2 + a * b + b * a + b2
= a2 + 2 * a * b + b2
Câu hỏi trang 10 SGK Toán 8 tập 1
Tính [a + (-b)]2 (với a, b là các số tùy ý).
Hướng dẫn giải
Áp dụng hằng đẳng thức bình phương của một tổng ta có:
[a + (-b)]2 = a2 + 2 * a * (-b) + (-b)2 = a2 – 2 * a * b + b2
Câu hỏi trang 11 SGK Toán 8 tập 1
Ai đúng, ai sai ?
a2 – 10a + 25 = (a – 5)2
Thọ viết:
a2 – 10 * a + 25 = (5 – a)2.
Hương nêu nhận xét: Thọ viết sai, Đức viết đúng.
Sơn nói: Qua ví dụ trên mình rút ra được một hằng đẳng thức rất đẹp!
Hãy nêu ý kiến của em. Sơn rút ra được hằng đẳng thức nào ?
Hướng dẫn giải
Đức và Thọ đều viết đúng;
Hương nhận xét sai;
Sơn rút ra được hằng đẳng thức là: (a – 5)2 = (5 – a)2
Bài tập 16 trang 11 SGK Toán 8 tập 1
Viết các biểu thức sau đây dưới dạng bình phương của một tổng hoặc một hiệu:
a) a2 + 2a + 1
b) 9a2 + b2 + 6ab
c) 25a2 + 4b2 – 20ab
d) a2 – a + 1/4
Hướng dẫn giải
a) Áp dụng hằng đẳng thức (hawngf ddawngr thuwcs) bình phương của một tổng với A = a và B = 1
a2 + 2a + 1
= a2 + 2a1 + (1)2
= (a + 1)2
b) Áp dụng hằng đẳng thức (hawngf ddawngr thuwcs) bình phương của một tổng với A = 3a và B = b
9a2 + b2 + 6ab
= 9a2 + 6ab + b2
= (3a)2 + 2.3ab + b2
= (3a + b)2
c) Áp dụng hằng đẳng thức (hawngf ddawngr thuwcs) bình phương của một hiệu với A = 5a và B = 2b
25a2 + 4b2 – 20ab
= 25a2 – 20ab + 4b2
= (5a)2 – 2 * 5a * 2b + (2b)2
= (5a – 2b)2
d) Áp dụng hằng đẳng thức (hawngf ddawngr thuwcs) bình phương của một hiệu với với A = a và B = 1/2
a2 – a + 1/4
= a2 – 2 * a * 1/2 + (1/2)2
= (a – 1/2)2

Với những chia sẻ vừa rồi của Chúng Tôi, hy vọng bạn đã nắm rõ 7 hằng đẳng thức (hawngf ddawngr thuwcs) đáng nhớ. Đừng quên theo dõi Chúng Tôi để không bỏ qua những kiến thức thú vị.
Trong bài viết trên, chúng ta đã tìm hiểu về 7 hằng đẳng thức đáng nhớ trong hình học phẳng. Những hằng đẳng thức này không chỉ đơn giản là các công thức tính toán mà còn mang ý nghĩa về quan hệ giữa các độ dài và góc trong các hình học học hình học.
Qua việc áp dụng và trực quan hóa các hằng đẳng thức trong bài tập, chúng ta có thể thấy rằng hằng đẳng thức không chỉ giúp chúng ta tính toán một cách chính xác mà còn giúp chúng ta hiểu biết sâu hơn về mối quan hệ giữa các yếu tố trong hình học.
Một trong những hằng đẳng thức quan trọng nhất là định lí Cosin. Hằng đẳng thức này cho phép chúng ta tính được một cạnh của tam giác khi biết độ dài hai cạnh khác và cosin của một góc. Việc áp dụng định lí Cosin không chỉ giúp giải quyết các bài toán tính toán mà còn hỗ trợ chúng ta điều tra và giải thích những đặc tính của các tam giác.
Sau đó, chúng ta đã tìm hiểu về các định lí Sin, Tan trong tam giác vuông. Những định lí này cùng với định lí Pytago đã giúp chúng ta tính được độ dài các cạnh còn lại và các góc trong tam giác vuông. Việc hiểu rõ và áp dụng thành thạo các định lí này sẽ giúp ta giải quyết các bài toán liên quan đến tam giác vuông một cách nhanh chóng và chính xác.
Bên cạnh đó, chúng ta cũng đã tìm hiểu về các hằng đẳng thức trong các tam giác đều và tam giác đồng quy. Những hằng đẳng thức này cho phép chúng ta tính được các góc trong tam giác và đặc biệt là tìm được độ dài các đoạn thẳng bằng nhau. Việc hiểu và áp dụng thành thạo các hằng đẳng thức này sẽ giúp chúng ta giải quyết các bài toán liên quan đến các tam giác đều và tam giác đồng quy một cách dễ dàng.
Từ việc nắm vững và áp dụng thành thạo những hằng đẳng thức này, chúng ta có thể giải quyết được nhiều bài toán trong hình học phẳng một cách hiệu quả. Đồng thời, việc hiểu biết sâu hơn về quan hệ giữa các độ dài và góc trong hình học cũng giúp chúng ta phát triển tư duy logic và khả năng tư duy trừu tượng.
Tổng kết lại, việc rèn luyện và hiểu sâu hơn về 7 hằng đẳng thức đáng nhớ trong hình học phẳng là điều cần thiết để nâng cao khả năng giải quyết các bài toán và tăng cường khả năng tư duy logic. Chúng ta hãy nắm vững và áp dụng thành thạo những hằng đẳng thức này để trở thành những người giỏi trong lĩnh vực hình học.
Cảm ơn bạn đã xem bài viết Hawngf ddawngr thuwcs – Bài tập về 7 hằng đẳng thức đáng nhớ tại Thcslytutrongst.edu.vn bạn có thể bình luận, xem thêm các bài viết liên quan ở phía dưới và mong rằng sẽ giúp ích cho bạn những thông tin thú vị.
Từ Khoá Liên Quan:
1. Định lí cơ bản về hạng đẳng thức
2. Bất đẳng thức tam giác đối với các đa giác
3. Hệ thức Chebyshev
4. Ung thư Chebyshev
5. Bất đẳng thức Cauchy-Schwarz
6. Bất đẳng thức đồng dạng
7. Chứng minh bằng phương pháp hợp
8. Bất đẳng thức AM-GM
9. Định lí tối đa tối tiểu
10. Bất đẳng thức Jensen
11. Bất đẳng thức Bernoulli
12. Bất đẳng thức Holder
13. Bất đẳng thức Minkowski
14. Định lí biến đổi tổ hợp
15. Bất đẳng thức Newton.


