Bạn đang xem bài viết Đường trung tuyến là gì? Công thức tính đường trung tuyến tại Thcslytutrongst.edu.vn bạn có thể truy cập nhanh thông tin cần thiết tại phần mục lục bài viết phía dưới.
Tìm hiểu về công thức tính đường trung tuyến trong chương trình Hình học trung học cơ sở. Nếu nắm được công thức tính đường trung tuyến sẽ giải các dạng bài tập liên quan về hình học tốt hơn. Mời các bạn học sinh theo dõi và ghi nhớ công thức tính đường trung tuyến và nhiều thông tin liên quan khác.

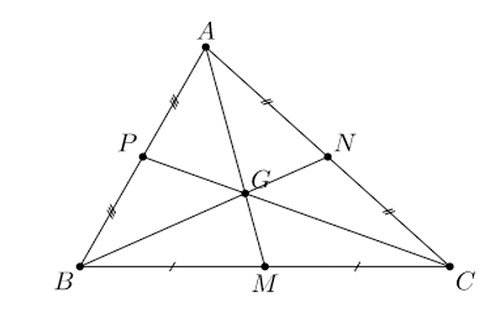
Trung tuyến tam giác là gì?
Trung tuyến 1 tam giác là một đoạn thẳng nối từ đỉnh tam giác tới trung điểm của cạnh đối diện. Mỗi tam giác sẽ có ba trung tuyến.
Đường trung tuyến là gì?
Đường trung tuyến được định nghĩa rõ ràng và ngắn gọn như sau: Đường trung tuyến 1 đoạn thẳng là một đường thẳng sễ đi qua trung điểm của đoạn thẳng đó.
Tính chất đường trung tuyến trong tam giác
Ba đường trung tuyến của tam giác sẽ cùng đi qua một điểm. Điểm đó sẽ có khoảng cách với đỉnh bằng 2/3 độ dài đường trung tuyến đi qua đỉnh đó. Giao điểm của ba đường trung tuyến chúng ta gọi là trọng tâm.
Minh họa bằng hình ảnh bên dưới:

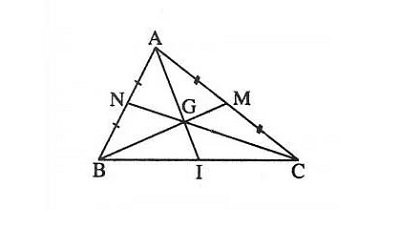
Với G là trọng tâm tam giác ABC (hình ảnh), ABC có một số trung tuyến đó là AI, BM, CN suy ra chúng ta sẽ có các biểu thức như sau AG/AI=BG/BM=CG/CN=2/3.
Công thức tính đường trung tuyến tam giác vuông
Tam giác vuông là tam giác mà nó có góc là góc vuông (90 độ). Đường trung tuyến của tam giác vuông sẽ mang các tính chất của một đường trung tuyến tam giác.
Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền sẽ bằng một nửa cạnh huyền.
Suy luận ra nếu một tam giác đường trung tuyến ứng với một cạnh bằng nửa cạnh đó, tam giác ấy khẳng định sẽ là tam giác vuông.
Ví dụ:
Cho tam giác ABC vuông tại B, độ dài của đường trung tuyến BM sẽ bằng MA, MC và bằng 1/2 AC. Nếu BM = 1/2 AC thì ta suy ra rằng tam giác ABC sẽ có 1 góc vuông đó là góc B.
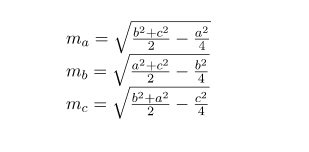
Công thức tính đường trung tuyến như sau:

Tính chất ba đường trung tuyến tam giác
Định lý: Ba đường trung tuyến của tam giác khi cùng đi qua điểm, điểm đó sẽ cách đỉnh một khoảng bằng 2/3 độ dài đường trung tuyến đi qua đỉnh ấy.
Giao điểm khi ba đường trung tuyến đi qua một điểm được gọi là trọng tâm.

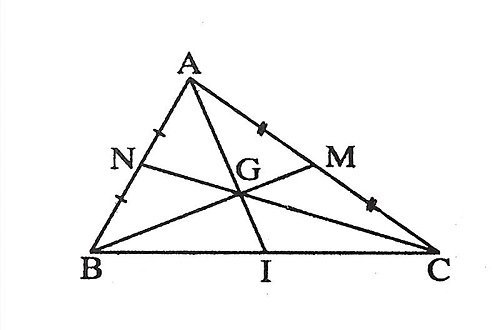
GT : với G là trọng tâm ∆ ABC
Suy ra rằng AG/AD=BG/BE=CG/CF=2/3
Bài tập đường trung tuyến
Học sinh hãy thực hành một số bài tập đơn giản về đường trung tuyến ngay bên dưới.
Bài 1: Tam giác ABC cân ở A, khi đó AB = AC = 17cm, BC= 16cm. Kẻ trung tuyến AM.
a) Chứng minh rằng AM ⊥ BC;
b) Tính độ dài của đường trung tuyến AM.
Bài 2: Cho G là trọng tâm ctam giác đều ABC. Chứng minh như sau GA = GB = GC.
Bài 3: Cho tam giác ABC, với trung tuyến BM. Trên tia BM lấy hai điểm G và K sao cho chúng ta có BG = BM và G là trung điểm đoạn BK. Gọi N trung điểm của KC , GN cắt CM ở O. Hãy chứng minh như sau:
a) O là trọng tâm tam giác GKC ;
b) GO = 1/3.BC
Bài 4: Cho tam giác ABC vuông tại A, ta có AB = 18cm, AC = 24cm. Tính khoảng cách từ trọng tâm G tam giác đến vị trí đỉnh của tam giác.
Bài 5: Tam giác ABC có trung tuyến AM. Cho biết rằng đoạn AM = ½BC. Chứng minh tam giác ABC vuông ở A.
Bài 6: Cho tam giác ABC. Trên tia đối của tia BA lấy điểm D để BD = BA. Cạnh BC lấy điểm E để BE = 1/3 BC. Gọi K chính là giao điểm AE và CD. Hãy chứng minh DK = KC.
Bài 7: Cho tam giác ABC ⊥ A, đường trung tuyến AM. Trên tia đối tia MA lấy điểm M sao cho MD = MA.
a) Tính số đo góc ABD.
b) Chứng minh rằng: ∆ABC = ∆BAD.
c) So sánh độ dài của đoạn AM và BC.
Bài 8
Tam giác ABC có đường trung tuyến AM, AM sẽ có độ dài bằng nửa cạnh BC. Chứng minh rằng góc BAC = 90∘.
Thực hành các bài tập đường trung tuyến cơ bản bên trên sẽ giúp học sinh biết cách thực hiện các bài tập về hình học.
Xem thêm: Công thức tính diện tích tam giác: Thường, Vuông, Cân, Đều
Chúng tôi vừa giới thiệu lại kiến thức đường trung tuyến, tính chất và công thức tính đường trung tuyến trong tam giác vuông, tam giác thường. Đây là công thức cơ bản mà học sinh cần nắm rõ khi làm quen với đường trung tuyến trong chương trình hình học trung học.
Cảm ơn bạn đã xem bài viết Đường trung tuyến là gì? Công thức tính đường trung tuyến tại Thcslytutrongst.edu.vn bạn có thể bình luận, xem thêm các bài viết liên quan ở phía dưới và mong rằng sẽ giúp ích cho bạn những thông tin thú vị.