7 hằng đẳng thức đáng nhớ cơ bản và mở rộng

Hằng đẳng thức là một phương trình đúng với mọi giá trị của biến số trong phạm vi xác định của nó. Hằng đẳng thức thường được sử dụng trong toán học để thể hiện một mối quan hệ giữa các biến số.

Ví dụ, một trong những hằng đẳng thức cơ bản nhất trong đại số là:

(a + b)^2 = a^2 + 2ab + b^2

Hằng đẳng thức này cho biết rằng bình phương của tổng hai số a và b bằng tổng của bình phương của số a, bình phương của số b và gấp đôi tích của a và b. Hằng đẳng thức này có thể được sử dụng để giải các bài toán liên quan đến bình phương và tổng hai số.

Một số hằng đẳng thức khác bao gồm hằng đẳng thức sin^2(x) + cos^2(x) = 1, hằng đẳng thức e^(iπ) + 1 = 0 (còn được gọi là công thức Euler), và hằng đẳng thức d’Euler cho đa giác lồi.

Trong chương trình học trung học cơ sở, phổ thông các em đều đã được làm quen với những đẳng thức toán học, trong đó 7 hằng đẳng thức đáng nhớ là những kiến thức quan trọng nhất các em cần phải nắm rõ. Những hằng đẳng thức này sẽ đi theo các em suốt quá trình học tập cho đến khi tốt nghiệp 12. Thế nên các em cần nắm vững phần lý thuyết và bài tập liên quan đến những hằng đẳng thức này để vượt qua các kỳ thi toán sắp tới. Dưới đây là 7 hằng đẳng thức đáng nhớ và mở rộng cùng với các bài tập mẫu và cách giải để các em tham khảo thêm.

7 hằng đẳng thức đáng nhớ cơ bản

Hằng đẳng thức là một tuyên bố về mối quan hệ giữa các toán hạng trong một biểu thức. Nói cách khác, hằng đẳng thức là một phương trình đúng cho mọi giá trị của các biến số trong đó.

Hằng đẳng thức có thể được chứng minh bằng nhiều phương pháp khác nhau, chẳng hạn như chứng minh trực tiếp, chứng minh bằng phương pháp đối chứng, chứng minh bằng định nghĩa, hoặc chứng minh bằng cách sử dụng các hằng đẳng thức và kết quả đã được chứng minh trước đó.

Trong toán học, các hằng đẳng thức đóng vai trò quan trọng trong việc giải quyết các bài toán, tính toán và phát triển lý thuyết. Một số hằng đẳng thức phổ biến được sử dụng trong nhiều lĩnh vực của toán học như đại số, hình học, giải tích, xác suất và thống kê.

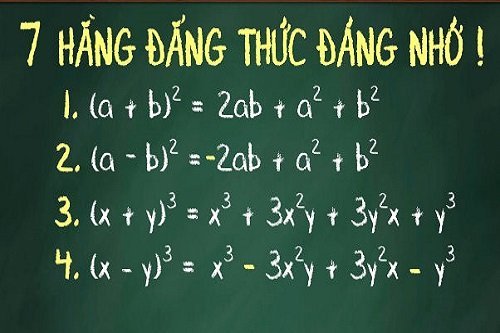
1. Bình phương của 1 tổng

(a+b)² = a² + 2ab + b²

Công thức bình phương của tổng (a + b)^2 là:

(a + b)^2 = a^2 + 2ab + b^2

Công thức này được gọi là công thức bình phương của tổng đơn giản, và có thể được chứng minh bằng cách sử dụng định nghĩa của bình phương, tức là:

(a + b)^2 = (a + b) x (a + b) = a(a + b) + b(a + b) = a^2 + ab + ab + b^2 = a^2 + 2ab + b^2

Trong đó, ta đã sử dụng phép nhân đơn giản để tích của hai tổng (a + b) và (a + b), rồi áp dụng phân phối nhân để tính toán các số hạng. Cuối cùng, ta thực hiện các phép tính đơn giản để tổng hợp các số hạng lại với nhau và thu được kết quả như trên.

2. Bình phương của một hiệu

(a-b)² = a² – 2ab + b²

Công thức bình phương của hiệu (a – b)^2 là:

(a – b)^2 = a^2 – 2ab + b^2

Công thức này cũng có thể được chứng minh bằng cách sử dụng định nghĩa của bình phương, tương tự như công thức bình phương của tổng. Ta có:

(a – b)^2 = (a – b) x (a – b) = a(a – b) – b(a – b) = a^2 – ab – ab + b^2 = a^2 – 2ab + b^2

Trong đó, ta cũng sử dụng phân phối nhân và các phép tính đơn giản để thu được kết quả như trên.

3. Hiệu 2 bình phương

a² – b² = (a-b) (a+b)

Công thức a^2 – b^2 = (a – b)(a + b) được gọi là công thức hiệu hai bình phương, và có thể được chứng minh bằng cách sử dụng định nghĩa của bình phương. Ta có:

(a – b)(a + b) = a(a + b) – b(a + b) = a^2 + ab – ab – b^2 = a^2 – b^2

Ở đây, ta sử dụng phép nhân đơn giản để tích của hai biểu thức (a – b) và (a + b), rồi áp dụng phân phối nhân để tính toán các số hạng. Cuối cùng, ta thực hiện các phép tính đơn giản để tổng hợp các số hạng lại với nhau và thu được kết quả như trên.

4. Lập phương của một tổng

(a+b)³ = a³ + 3a²b + 3ab² + b³

Công thức lập phương của tổng (a + b)^3 là:

(a + b)^3 = a^3 + 3a^2b + 3ab^2 + b^3

Công thức này cũng có thể được chứng minh bằng cách sử dụng định nghĩa của lập phương. Ta có:

(a + b)^3 = (a + b)^2 x (a + b) = (a^2 + 2ab + b^2)(a + b) = a^3 + 2a^2b + ab^2 + 2a^2b + 4ab^2 + 2b^3 = a^3 + 3a^2b + 3ab^2 + b^3

Ở đây, ta sử dụng công thức bình phương của tổng để tính toán (a + b)^2, rồi áp dụng tính chất phân phối nhân để tính toán (a^2 + 2ab + b^2)(a + b) thành các số hạng tương ứng. Cuối cùng, ta thực hiện các phép tính đơn giản để tổng hợp các số hạng lại với nhau và thu được kết quả như trên.

5. Lập phương của một hiệu

(a-b)³ = a³ – 3a²b + 3ab² + b³

Công thức lập phương của hiệu (a – b)^3 là:

(a – b)^3 = a^3 – 3a^2b + 3ab^2 – b^3

Công thức này cũng có thể được chứng minh bằng cách sử dụng định nghĩa của lập phương. Ta có:

(a – b)^3 = (a – b)^2 x (a – b) = (a^2 – 2ab + b^2)(a – b) = a^3 – 2a^2b + ab^2 – 2a^2b + 4ab^2 – 2b^3 = a^3 – 3a^2b + 3ab^2 – b^3

Ở đây, ta sử dụng công thức bình phương của hiệu để tính toán (a – b)^2, rồi áp dụng tính chất phân phối nhân để tính toán (a^2 – 2ab + b^2)(a – b) thành các số hạng tương ứng. Cuối cùng, ta thực hiện các phép tính đơn giản để tổng hợp các số hạng lại với nhau và thu được kết quả như trên.

6. Tổng hai lập phương

a³ + b³ = (a + b) (a² – ab + b²)

Công thức cho tổng hai lập phương là:

a^3 + b^3 = (a + b)(a^2 – ab + b^2)

Công thức này có thể được chứng minh bằng cách sử dụng định nghĩa của tổng hai lập phương. Ta có:

a^3 + b^3 = (a + b)(a^2 – ab + b^2)

= a^3 + a^2b – a^2b – ab^2 + ab^2 + b^3

= a^3 + b^3

Ở đây, ta sử dụng tính chất phân phối nhân để tính toán (a + b)(a^2 – ab + b^2) thành các số hạng tương ứng. Sau đó, ta thực hiện các phép tính đơn giản để tổng hợp các số hạng lại với nhau và thu được kết quả như trên.

7. Hiệu hai lập phương

a³ – b³ = (a – b) (a² + ab + b²)

Công thức cho hiệu hai lập phương là:

a^3 – b^3 = (a – b)(a^2 + ab + b^2)

Công thức này có thể được chứng minh bằng cách sử dụng định nghĩa của hiệu hai lập phương. Ta có:

a^3 – b^3 = (a – b)(a^2 + ab + b^2)

= a^3 – a^2b + ab^2 – a^2b + ab^2 – b^3

= a^3 – b^3

Ở đây, ta sử dụng tính chất phân phối nhân để tính toán (a – b)(a^2 + ab + b^2) thành các số hạng tương ứng. Sau đó, ta thực hiện các phép tính đơn giản để tổng hợp các số hạng lại với nhau và thu được kết quả như trên.

Các hằng đẳng thức mở rộng

1. Hằng đẳng thức bậc hai

Hằng đẳng thức bậc hai mở rộng là một dạng mở rộng của hằng đẳng thức bậc hai cơ bản. Nó được sử dụng để tính toán bình phương của các biểu thức chứa nhiều hơn hai số.

Hằng đẳng thức bậc hai mở rộng cho phép tính bình phương của một tổng nhiều số dưới dạng tổng các bình phương và các tích của các số ban đầu. Cụ thể, công thức của hằng đẳng thức bậc hai mở rộng là:

(a1 + a2 + … + an)^2 = a1^2 + a2^2 + … + an^2 + 2(a1a2 + a1a3 + … + a1an + a2a3 + … + a2an + … + an-1an)

Trong đó, a1, a2, …, an là các số bất kỳ. Công thức này có thể được sử dụng để tính bình phương của các biểu thức chứa nhiều hơn hai số.

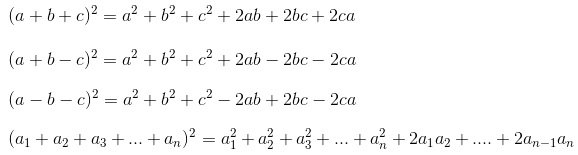
2. Hằng đẳng thức bậc ba

Hằng đẳng thức bậc ba mở rộng là một dạng mở rộng của hằng đẳng thức bậc ba cơ bản. Nó được sử dụng để tính toán lập phương của các biểu thức chứa nhiều hơn hai số.

Công thức của hằng đẳng thức bậc ba mở rộng là:

(a1 + a2 + … + an)^3 = a1^3 + a2^3 + … + an^3 + 3(a1^2a2 + a1^2a3 + … + a1^2an + a1a2^2 + a1a3^2 + … + a1an^2 + a2^2a3 + … + a2^2an + a2a3^2 + … + a2an^2 + … + an-1^2an)

Trong đó, a1, a2, …, an là các số bất kỳ. Công thức này có thể được sử dụng để tính lập phương của các biểu thức chứa nhiều hơn hai số.

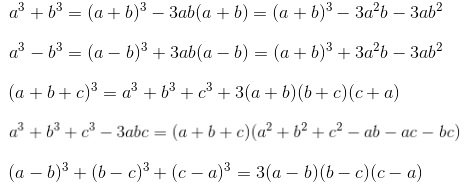
3. Hằng đẳng thức mở rộng khác

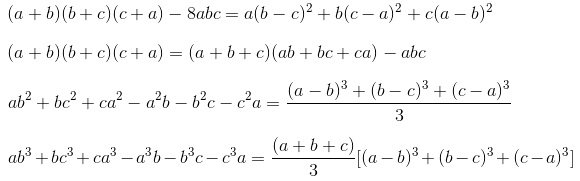
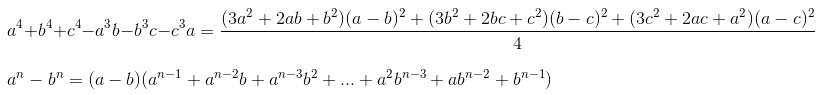
Đối với n là số lẽ thì chúng ta áp dụng công thức phía dưới:

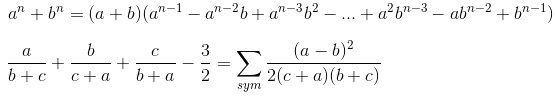
Ngoài các hằng đẳng thức bậc hai và ba đã được giới thiệu, còn có nhiều hằng đẳng thức khác cũng rất quan trọng và được sử dụng rộng rãi trong toán học. Một số hằng đẳng thức mở rộng đáng chú ý khác bao gồm:

• Hằng đẳng thức bậc tư mở rộng: (a + b + c + d)^4 = a^4 + b^4 + c^4 + d^4 + 4(a^3b + a^3c + a^3d + b^3a + b^3c + b^3d + c^3a + c^3b + c^3d + d^3a + d^3b + d^3c) + 6(a^2b^2 + a^2c^2 + a^2d^2 + b^2c^2 + b^2d^2 + c^2d^2) + 12(a^2bc + a^2bd + a^2cd + b^2ac + b^2ad + b^2cd + c^2ab + c^2ad + c^2bd + d^2ab + d^2ac + d^2bc)
• Hằng đẳng thức Laplace mở rộng: Đây là một dạng mở rộng của hằng đẳng thức bậc hai và được sử dụng trong đại số tuyến tính. Công thức của hằng đẳng thức Laplace mở rộng phụ thuộc vào kích thước của ma trận và khá phức tạp, tuy nhiên nó rất hữu ích trong việc tính toán đại số tuyến tính.
• Hằng đẳng thức Vandermonde mở rộng: Đây là một dạng mở rộng của hằng đẳng thức bậc nhất và được sử dụng trong đại số tuyến tính và giải tích số. Công thức của hằng đẳng thức Vandermonde mở rộng cũng phụ thuộc vào kích thước của ma trận và khá phức tạp.

4. Nhị thức Newton

Nhị thức Newton là một công thức toán học cực kỳ quan trọng trong đại số và lý thuyết xác suất, được đặt theo tên nhà toán học người Anh Isaac Newton. Công thức này được sử dụng để tính giá trị của biểu thức (a + b)^n, trong đó a, b là hai số bất kỳ và n là một số nguyên không âm. Công thức có dạng:

(a + b)^n = C(n,0)a^nb^0 + C(n,1)*a^(n-1)*b^1 + C(n,2)*a^(n-2)*b^2 + … + C(n,n)a^0b^n

Trong đó, C(n, k) là số tổ hợp chập k của n phần tử, được tính bằng công thức:

C(n, k) = n! / (k! * (n-k)!)

trong đó, n! là giai thừa của n, và k! là giai thừa của k. Biểu thức (a + b)^n là tổng của các thành phần a^k*b^(n-k) nhân với số tổ hợp chập k của n phần tử. Công thức này có thể được chứng minh bằng cách sử dụng định nghĩa của số tổ hợp chập k và áp dụng định lý nhị thức của Pascal.

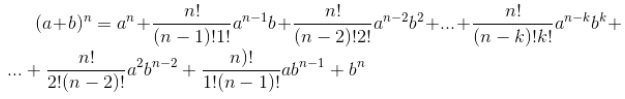
Các dạng bài tập ứng dụng 7 hằng đẳng thức đáng nhớ và cách giải

Dạng 1: Tính giá trị của biểu thức cho trước

Tính giá trị của biểu thức sau:

A = x² – 4x + 4 tại x = -1

Ta có : A = x² – 4x + 4 = A = x² – 2.x.2 + 2² = (x – 2)²
Tại x = -1 : A = ((-1) – 2)²=(-3)²= 9
Vậy : A(-1) = 9

Dạng 2: Chứng minh giá trị biểu thức B không phụ thuộc vào biến x

B = (x – 1)² + (x + 1)(3 – x)

LỜI GIẢI:

B =(x – 1)² + (x + 1)(3 – x)
= x² – 2x + 1 – x² + 3x + 3 – x
= 4 : là hằng số không phụ thuộc vào biến x.

Dạng 3: Tìm giá trị nhỏ nhất của biểu thức

C = x² – 2x + 5

GIẢI:

Ta có : C = x² – 2x + 5 = (x² – 2x + 1) + 4 = (x – 1)² + 4
Mà : (x – 1)² ≥ 0 với mọi x.
=> (x – 1)² + 4 ≥ 4 hay C ≥ 4
Dấu “=” xảy ra khi : x – 1 = 0 <=> x = 1
Nên vì vậy : Cmin = 4 khi x = 1

Dạng 4: Tìm giá trị lớn nhất của biểu thức D

D = 4x – x²

LỜI GIẢI:

Ta có : D = 4x – x² = 4 – 4 + 4x – x² = 4 – (4 + x² – 4x) = 4 – (x – 2)²
Mà ta có: -(x – 2)² ≤ 0 với mọi x.
Suy ra : 4 – (x – 2)² ≤ 4 hay D ≤ 4
Dấu “=” xảy ra khi : x – 2 = 0 <=> x = 2
Nên giá trị lớn nhất của D: Dmax = 4 khi x = 2.

Dạng 5: Chứng minh đẳng thức

(a + b)³ – (a – b)³ = 2b(3a² + b²)

LỜI GIẢI:

VT = (a + b)³ – (a – b)³
= (a³ + 3a²b + 3ab² + b³) – (a³ – 3a²b + 3ab² – b³)
= a³ + 3a²b + 3ab² + b³ – a³ + 3a²b – 3ab² + b³
= 6a²b + 2b³
= 2b(3a² + b²) =>đpcm.
=> (a + b)³ – (a – b)³ = 2b(3a² + b²)

Dang 6: Phân tích các đa thức thành nhân tử

F = x² – 4x + 4 – y²

Lời Giải:

Ta có : F = x² – 4x + 4 – y²
= (x² – 4x + 4) – y² [nhóm các hạng tử]
= (x – 2)² – y² [hằng đẳng thức số 2]
= (x – 2 – y )( x – 2 + y) [ hằng đẳng thức số 3]
=> F = (x – 2 – y )( x – 2 + y)

Bài số 1 :

A = x³ – 4×2 + 4x
= x.(x² – 4x + 4)
= x.(x² – 2.2x + 2²)
= x(x – 2)²

Bài số 2 :

B = x² – 2xy – x + 2y
= (x²– x) + (2y – 2xy)
= x.(x – 1) – 2y.(x – 1)
= (x – 1)(x – 2y)

Bài số 3 :

C = x² – 5x + 6
= x² – 2x – 3x + 6
= x(x – 2) – 3(x – 2)
= (x – 2)(x – 3)

Dạng 7: Tìm x, biết : x².( x – 3 ) – 4x + 12 = 0

Lời Giải:

x² ( x – 3 ) – 4x + 12 = 0
<=> x² ( x – 3 ) – 4(x – 3 ) = 0
<=>( x – 3 ) (x² – 4) = 0
<=>( x – 3 ) (x – 2)(x + 2) = 0
<=>( x – 3 ) = 0 hay (x – 2) = 0 hay (x + 2) = 0
<=> x = 3 hay x = 2 hay x = –2
vậy : x = 3; x = 2; x = –2

Tìm x:

2x² – 5x = 0
<=>2x(x – 5) = 0
<=>2x = 0 hoặc x – 5 = 0
<=>x = 0 hoặc x = 5

x³ – 5x² + 6x = 0
<=> x(x² – 5x + 6) = 0
<=> x(x – 2)(x – 3) = 0
<=> x = 0 hay x – 2 = 0 hay x – 3 = 0
<=> x = 0 hay x = 2 hay x = 3

Dạng 8: Chứng minh bất đẳng thức trong toán thi vào lớp 10

Bài toán 1 : Chứng minh bất đẳng thức sau:
a²/4+ b² ≥ ab

Lời Giải:

Xét: VT – VP = a²/4+ b² – ab = (a/2)² – 2ba/2 + b2 = (a – b)²
Ta luôn có : (a – b)² ≥ 0 với mọi giá trị a,b thuộc R
Suy ra : VT – VP ≥ 0
Vậy : a²/4+ b² ≥ ab

Bài toán 2 : Chứng minh bất đẳng thức sau:
a² + b² + c² ≥ ab + bc + ac với mọi a, b,c thuộc R

Lời Giải:

Xét :VT – VP = a² + b² + c² – ab – bc – ac
2(VT – VP) = 2(a² + b² + c² – ab – bc – ac)
= (a² – 2ab + b²) + (a² – 2ac + c²) + (b² – 2bc + c²)
= (a – b)² + (a – c)² + (b – c)²
Ta luôn có rằng : (a – b)² ≥ 0 với mọi a,b thuộc R
(a – c)² ≥ 0 với mọi giá trị a,c thuộc R
(b – c)² ≥ 0 với mọi giá trị b,c thuộc R
Suy ra : (a – b)² + (a – c)² + (b – c)² ≥ 0 với mọi a, b,c thuộc R
Hay : VT – VP = a² + b² + c² – ab – bc – ac ≥ 0 với mọi a, b,c thuộc R
Vậy : a² + b² + c² ≥ ab + bc + ac

Bài toán 3 : Chứng minh bất đẳng thức sau
a⁴ + b⁴ ≥ a³b + ab³

Lời Giải:

Xét :VT – VP = a⁴ + b⁴ – a³b – ab³
= (a⁴ – a³b) + (b⁴– ab³)
= a³(a – b) – b³(a – b)
= (a – b) (a³– b³)
= (a – b)² (a²+ ab + b²) = (a – b)² [(a+b/2)² + 3b²/4)]
Ta luôn có rằng : (a – b)² ≥ 0 với mọi giá trị a,b thuộc R
(a+b/2)² + 3b²/4) ≥ 0 với mọi giá trị a,b thuộc R
Suy ra : VT – VP ≥ 0
Vậy ta có: a⁴ + b⁴ ≥ a³b + ab³

Các dạng bài tập ứng dụng 7 hằng đẳng thức đáng nhớ thường liên quan đến việc tìm giá trị của biểu thức chứa các biến số. Dưới đây là một số dạng bài tập cụ thể và cách giải quyết:

1. Tìm giá trị của biểu thức bậc hai chứa hai biến số: Bài tập: Cho a và b là hai số thực khác không. Tính giá trị của biểu thức: A = (a + b)² + (a – b)². Giải quyết: Sử dụng hai hằng đẳng thức bậc hai, ta có: (a + b)² = a² + 2ab + b² (a – b)² = a² – 2ab + b² Thay vào biểu thức A, ta được: A = a² + 2ab + b² + a² – 2ab + b² = 2(a² + b²) Vậy giá trị của biểu thức A là 2(a² + b²).
2. Tìm giá trị của biểu thức bậc ba chứa hai biến số: Bài tập: Cho a và b là hai số thực khác không. Tính giá trị của biểu thức: A = (a + b)³ – (a – b)³. Giải quyết: Sử dụng hai hằng đẳng thức bậc ba, ta có: (a + b)³ = a³ + 3a²b + 3ab² + b³ (a – b)³ = a³ – 3a²b + 3ab² – b³ Thay vào biểu thức A, ta được: A = a³ + 3a²b + 3ab² + b³ – a³ + 3a²b – 3ab² + b³ = 6ab(a + b) Vậy giá trị của biểu thức A là 6ab(a + b).
3. Tìm giá trị của biểu thức chứa nhiều biến số: Bài tập: Cho a, b, c là các số thực khác không. Tính giá trị của biểu thức: A = a⁴ + b⁴ + c⁴ – 2a²b² – 2b²c² – 2c²a². Giải quyết: Sử dụng hằng đẳng thức bậc tư, ta có: (a² + b²)² = a⁴ + 2a²b² + b⁴ (b² + c²)² = b⁴ + 2b²c² + c⁴ (c² + a²)² = c⁴ + 2c²a² + a⁴ Thay vào biểu thức A, ta được: A = (a² + b²)² + (b² + c²)² + (c² + a²)² – 4a

7 hằng đẳng thức đáng nhớ cơ bản và mở rộng cùng với các dạng bài tập về hằng đẳng thức và cách giải trên đây hi vọng sẽ giúp các em tìm hiểu và mở rộng thêm nhiều kiến thức về hằng đẳng thức cho môn Toán học. Chúc các em học giỏi và vượt qua những kỳ thi một cách thuận lợi, thành công!