Bạn đang xem bài viết Công thức tính cạnh huyền tam giác vuông đầy đủ nhất tại Thcslytutrongst.edu.vn bạn có thể truy cập nhanh thông tin cần thiết tại phần mục lục bài viết phía dưới.
Trong toán học, tam giác vuông là một trong những hình học cơ bản được nghiên cứu rộng rãi. Đặc biệt, tính toán độ dài cạnh huyền của tam giác luôn là một vấn đề thu hút sự quan tâm và tò mò của nhiều học sinh và người học. Công thức tính cạnh huyền tam giác vuông đã được biết đến từ lâu và được áp dụng trong nhiều lĩnh vực khác nhau, từ hình học đến vật lý và kỹ thuật. Trong bài viết này, chúng ta sẽ tìm hiểu về công thức tính cạnh huyền tam giác vuông đầy đủ nhất và cách áp dụng nó vào các bài toán thực tế.
Đôi khi nhiều bạn học sinh quên cách tính cạnh huyền tam giác vuông. Do đó, bài viết hôm nay của Chúng Tôi sẽ giúp bạn khơi gợi lại công thức hình học này. Mời bạn đọc theo dõi nội dung sau để biết thêm chi tiết.
Cạnh huyền trong tam giác là gì?
Cạnh huyền chính là tên gọi của một cạnh trong tam giác. Điều đặc biệt, trong tam giác vuông cạnh huyền là cạnh đối diện với góc vuông. Cạnh này có độ dài lớn nhất trong 3 cạnh của một tam giác vuông.
Chắc hẳn qua thông tin trên bạn đã hình dung ra được cạnh huyền của một tam giác vuông. Nội dung sau sẽ bật mí giúp bạn công thức tính cạnh huyền tam giác vuông. Mời bạn đọc theo dõi cùng Chúng Tôi.
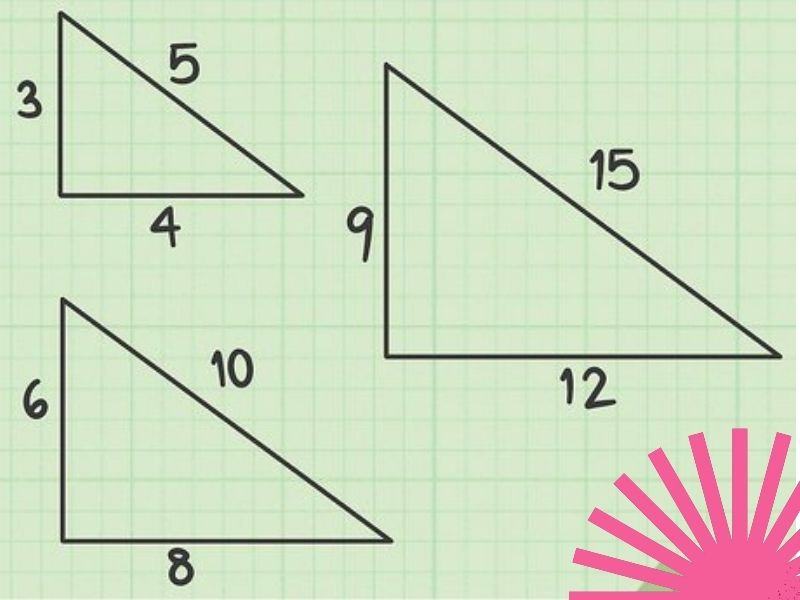
Công thức tính cạnh huyền tam giác vuông
Công thức tính cạnh huyền theo định lý Pytago
Theo định lý Pytago, một tam giác vuông bất kì có bình phương chiều dài cạnh huyền bằng tổng bình phương chiều dài hai cạnh góc vuông còn lại.
Công thức: c2 = a2 + b2
Trong đó:
- c: Cạnh huyền tam giác vuông.
- a,b: Lần lượt là 2 cạnh góc vuông còn lại.
Vừa rồi là công thức tính cạnh huyền tam giác vuông theo định lý Pytago. Mời bạn đọc đến với phần tiếp theo của bài viết đó chính là công thức tính cạnh huyền theo định lý Sin.

Công thức tính cạnh huyền theo định lý Sin
Sin thể hiện tỉ số giữa các góc hoặc các cạnh trong tam giác vuông. Theo định lý Sin, trong tam giác vuông sin của một góc được xác định bằng chiều dài của cạnh đối diện chia cho cạnh huyền.
Với tam giác bất kì có các cạnh a, b, c và các góc A, B, C thì theo định lý Sin ta có:
a/sin A = b/sin B = c/sin C
Chú ý: Định lý Sin có thể dùng để giải mọi tam giác, tuy nhiên riêng để tính cạnh huyền thì chỉ tam giác vuông mới có.
Nội dung trên là công thức tính cạnh huyền theo định lý Sin. Tiếp nối bài viết là thông tin về công thức tính cạnh huyền tam giác vuông đặc biệt. Mời bạn đọc cùng tham khảo.
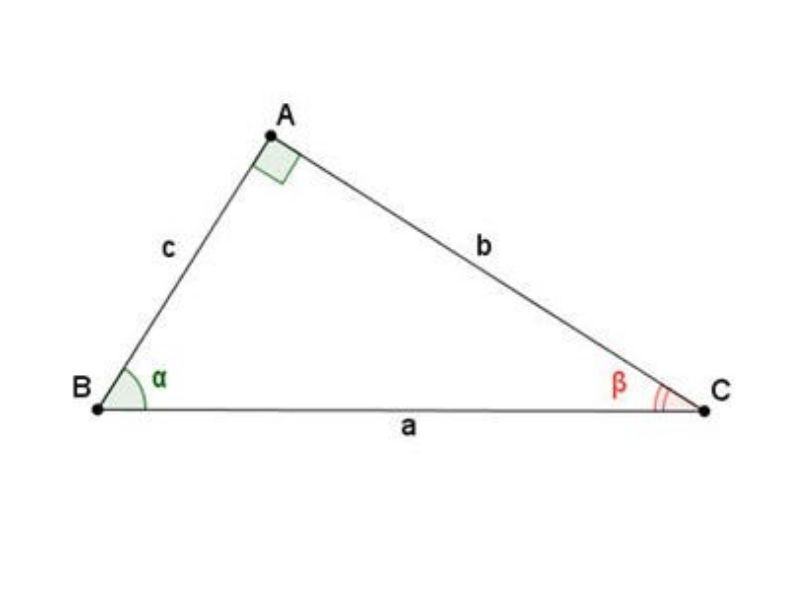
Công thức tính cạnh huyền trong tam giác vuông đặc biệt
Dưới đây là một số trường hợp đặc biệt khi tìm độ dài cạnh huyền của tam giác vuông:
- Bộ ba số Pytago chính là chiều dài các cạnh của tam giác vuông đặc biệt. Bộ số này là 3 – 4 – 5. Nếu thấy hai cạnh góc vuông của một tam giác vuông là 3 và 4 thì bạn có thể suy ra ngay cạnh huyền của tam giác đó bằng 5.
- Nếu tam vuông đặc biệt có số đo ba góc là 45 độ, 45 độ và 90 độ thì tam giác này là tam giác vuông cân.
- Cạnh của tam giác vuông đặc biệt có tỉ lệ 1:1:1. Điều này có nghĩa là hai cạnh góc vuông bằng nhau. Đồng thời, chiều dài cạnh huyền bằng chiều dài cạnh góc vuông nhân với căn bậc hai của hai.
- Nếu tam giác vuông đặc biệt có số đo ba góc bằng 30 – 60 – 90 thì các cạnh của tam giác này có tỉ lệ là x:x:2x. Nếu biết được chiều dài của một cạnh góc vuông thì có thể tìm ra được chiều dài cạnh huyền.
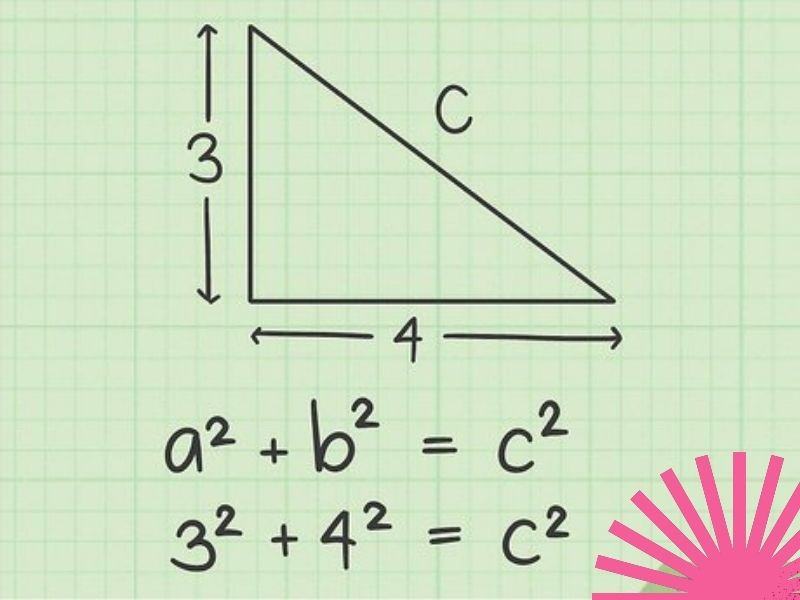
Vừa rồi là ba công thức tính cạnh huyền tam giác vuông mà bạn thường gặp. Do đó, các bạn học sinh nên ghi nhớ để việc giải Toán hình dễ dàng hơn. Sau đây là một số bài tập áp dụng công thức tính cạnh huyền trong tam giác vuông, mời bạn đọc cùng tham khảo.
Xem thêm: Công thức tính đường cao trong tam giác đều dễ nhớ nhất
Bài tập tham khảo về tính cạnh huyền tam giác vuông
Bài 1: Một tam giác vuông có chiều dài bằng 10cm, cạnh bên bằng 6cm. Hỏi cạnh còn lại bằng bao nhiêu?
Bài giải:
Ta có:
a = 6cm, c = 10cm
Theo định lý Pytago, ta có:
c2 = a2 + b2
102 = 62 + b2
100 = 36 + b2
=> b2 = 100 – 36
=> b2 = 64
=> b = 8cm
Đáp án: 8cm.
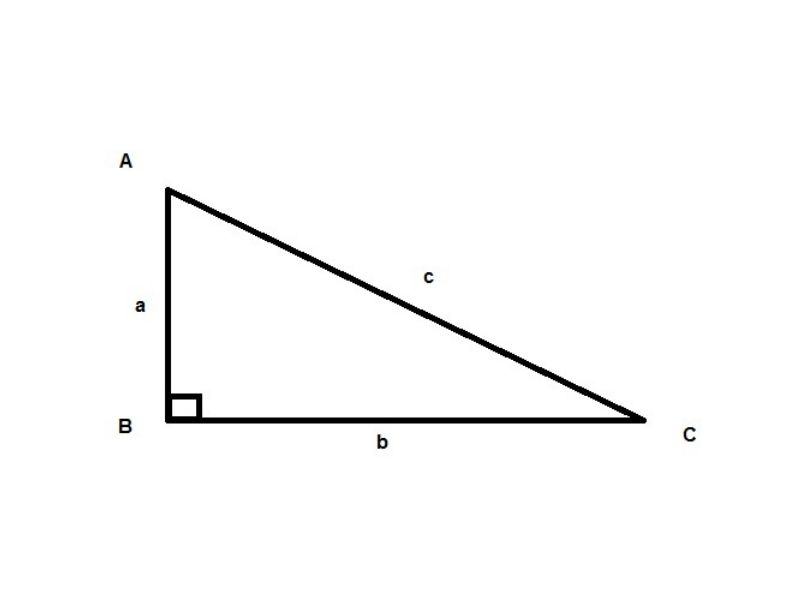
Bài 2: Cho ∆ABC vuông tại A, biết AB = 6cm, AC = 8cm. Hỏi BC bằng bao nhiêu?
Bài giải:
Theo định lý Pytago, ta có:
a = AB = 6cm, b = AC = 8cm
c2 = a2 + b2
= 62 + 82
= 36 + 64
= 100
=> c = 10cm
=> BC = 10cm
Đáp số: 10cm.
Hi vọng qua những bài tập vừa rồi sẽ giúp các bạn học sinh nhớ được công thức tính cạnh huyền tam giác vuông. Đừng quên share bài của Chúng Tôi để khi cần có thể xem lại nhé! Chúc các bạn có một buổi học thật hiệu quả.
Trong kết luận này, chúng ta sẽ tổng kết công thức tính cạnh huyền của tam giác vuông đầy đủ nhất.
Tam giác vuông là một trong những hình học cơ bản và quan trọng, nó có nhiều ứng dụng trong đa dạng lĩnh vực như vật lý, toán học và kỹ thuật. Cạnh huyền của tam giác vuông là cạnh đối diện với góc vuông, và việc tính toán cạnh huyền có thể gặp khó khăn khi ta không biết giá trị của nó.
Tuy nhiên, chúng ta có thể sử dụng công thức tính cạnh huyền tam giác vuông đầy đủ nhất – đó là định lý Pitago. Định lý này cho biết rằng trong một tam giác vuông, bình phương của cạnh huyền bằng tổng bình phương của hai cạnh góc vuông.
Công thức này được biểu diễn như sau: a^2 + b^2 = c^2, trong đó a và b là độ dài hai cạnh góc vuông, và c là độ dài cạnh huyền. Khi ta biết được giá trị hai cạnh góc vuông, ta có thể áp dụng công thức này để tính được cạnh huyền tam giác vuông một cách chính xác.
Ngoài ra, công thức cạnh huyền tam giác vuông cũng có thể được sử dụng theo ngược lại. Đó là, khi chúng ta biết giá trị của cạnh huyền và một trong hai cạnh góc vuông, ta có thể tìm được giá trị của cạnh góc vuông còn lại bằng cách áp dụng công thức trên và giải phương trình.
Việc tính toán cạnh huyền tam giác vuông đầy đủ nhất có thể có nhiều ứng dụng trong thực tế. Ví dụ, trong lĩnh vực xây dựng, tính toán chiều dài cạnh huyền một tam giác vuông có thể giúp xác định kích thước và vị trí chính xác của các thành phần cấu trúc. Trong toán học, công thức này được sử dụng để giải các bài toán liên quan đến tam giác vuông và các hình học tương tự.
Tổng kết lại, công thức tính cạnh huyền tam giác vuông đầy đủ nhất được biểu diễn bằng định lý Pitago, là công thức quan trọng và hữu ích trong việc tính toán cạnh huyền của tam giác vuông. Việc biết cách áp dụng công thức này sẽ giúp chúng ta hiểu rõ hơn về tính chất và ứng dụng của tam giác vuông trong các lĩnh vực khác nhau.
Cảm ơn bạn đã xem bài viết Công thức tính cạnh huyền tam giác vuông đầy đủ nhất tại Thcslytutrongst.edu.vn bạn có thể bình luận, xem thêm các bài viết liên quan ở phía dưới và mong rằng sẽ giúp ích cho bạn những thông tin thú vị.
Từ Khoá Liên Quan:
1. Cạnh huyền tam giác vuông
2. Cạnh huyền tam giác vuông là gì
3. Tính công thức cạnh huyền tam giác vuông
4. Công thức tính cạnh huyền tam giác vuông
5. Công thức tính cạnh huyền tam giác vuông đầy đủ
6. Công thức tính cạnh huyền tam giác vuông chứa vào tam giác vuông
7. Công thức tính cạnh huyền tam giác vuông qua chiều cao tam giác vuông
8. Công thức tính cạnh huyền tam giác vuông qua đường tròn ngoại tiếp tam giác
9. Cách tính cạnh huyền tam giác vuông
10. Quy tắc tính cạnh huyền tam giác vuông
11. Bài toán tính cạnh huyền tam giác vuông
12. Định lý tính cạnh huyền tam giác vuông
13. Công thức tính cạnh huyền tam giác vuông dựa vào cạnh góc vuông và cạnh nhọn tam giác vuông
14. Bài toán tính cạnh huyền tam giác vuông sử dụng định lý Pythagoras
15. Công thức tính cạnh huyền tam giác vuông qua phân giác góc


