Bạn đang xem bài viết Phân tích đa thức thành nhân tử tại Thcslytutrongst.edu.vn bạn có thể truy cập nhanh thông tin cần thiết tại phần mục lục bài viết phía dưới.
Hướng dẫn giải bài tập Toán phân tích đa thức thành nhân tử, đây là tài liệu tham khảo vô cùng có ích cho các em học sinh khi giải Toán ngay tại lớp. Hãy theo dõi bài giải ngay dưới đây nhé.
1. Định nghĩa
Phân tích đa thức thành nhân tử (thừa số) có nghĩa là biến đổi đa thức đó thành một tích của những đa thức.
Ví dụ:
a) 2x2 + 5x – 3 = (2x – 1).(x + 3)
b) x – 2√xy +5√x – 10y = [(√x)2 – 2 y√x] + (5√x – 10y)
= √x(√x- 2y) + 5(√x- 2y)
= (√x- 2y)(√x + 5)
2. Phương pháp phân tích đa thức thành nhân tử
a) Phương pháp đặt nhân tử chung:
Nếu tất cả các hạng tử của đa thức có một nhân tử chung thì đa thức đó được biểu diễn thành một tích của nhân tử chung với một đa thức khác.
Công thức: AB + AC = A(B + C)
Ví dụ:
1. 5x(y + 1) – 2(y + 1) = (y + 1)(5x – 2)
2. 3x + 12√xy = 3√x(√x + 4y)
b) Phương pháp hằng đẳng thức:
Nếu đa thức là một vế hằng đẳng thức đáng nhớ nào đó thì có thể dùng hằng đẳng thức đó để biểu diễn đa thức này thành tích các đa thức.
* Các hằng đẳng thức đáng nhớ:
(A + B)2 = A2 + 2AB + B2
(A – B)2 = A2 – 2AB + B2
A2 – B2 = (A + B)(A – B)
(A+B)3= A3 + 3A2B + 3AB2 + B3
(A – B)3= A3 – 3A2B + 3AB2-B3
A3 + B3 = (A+B) (A2 – AB + B2)
A3 – B3 = (A – B)(A2 + AB + B2)
Ví dụ: Phân tích các đa thức sau thành nhân tử:
1. x2 – 4x + 4 = (x – 2)2
2. x2 – 9 = (x – 3)(x + 3)
3. (x + y)2 – (x – y)2 = [(x + y) + (x – y)][(x + y) – (x – y)] = 2x.2y = 4xy
Cách khác: (x + y)2 – (x – y)2 = x2 + 2xy + y2 – (x2 – 2xy + y2) = 4xy
c) Phương pháp nhóm hạng tử:
Nhóm một số hạng tử của một đa thức một cách thích hợp để có thể đặt được nhân tử chung hoặc dùng hằng đẳng thức đáng nhớ.
Ví dụ:
1. x2 – 2xy + 5x – 10y = (x2 – 2xy) + (5x – 10y)
= x(x – 2y) + 5(x – 2y)
= (x – 2y)(x + 5)
2. x – 3√x + √xy – 3y = (x – 3√x) + (√xy – 3y)
= √x(√x – 3) + y(√x – 3)
= (√x – 3)(√x + y)
d. Phương pháp tách một hạng tử: (trường hợp đặc biệt tam thức bậc 2 có nghiệm)
Tam thức bậc hai có dạng:

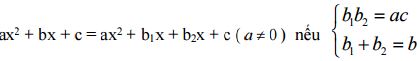
Ví dụ:
a) 2x2 – 3x + 1 = 2x2 – 2x – x +1
= 2x(x – 1) – (x – 1)
= (x – 1)(2x – 1)
b) y – 3√y + 2 = y – √y – 2√y + 2
= √y(√y – 1) – 2(√y – 1)
= (√y – 2)(y – 1)
e. Phương pháp thêm hoặc bớt cùng 1 hạng tử:
Ví dụ:
a) y4 + 64 = y4 + 16y2 + 64 – 16y2
= (y2 + 8)2 – (4y)2
= (y2 + 8 – 4y)(y2 + 8 + 4y)
b) x2 + 4 = x2 + 4x + 4 – 4x
= (x + 2)2 – 4x = (x + 2)2 – (2√x)2
= (x – 2√x + 2)(x + 2√x + 2)
g. Phương pháp phối hợp nhiều phương pháp:
Ví dụ:
a3 – a2b – ab2 + b3 = a2(a – b) – b2(a – b)
= (a – b) (a2 – b2)
= (a – b) (a – b) (a + b)
= (a – b)2(a + b)
Các em học sinh nên làm thêm một số bài tập dạng này hoặc tìm hiểu thêm các ví dụ minh họa để hiểu các cách phân tích nhé. Chúc các em học tốt môn Toán lớp 8.
Cảm ơn bạn đã xem bài viết Phân tích đa thức thành nhân tử tại Thcslytutrongst.edu.vn bạn có thể bình luận, xem thêm các bài viết liên quan ở phía dưới và mong rằng sẽ giúp ích cho bạn những thông tin thú vị.