Tâm đường tròn ngoại tiếp tam giác

Tâm đường tròn ngoại tiếp tam giác là một đường tròn nằm ngoài tam giác và liên tục với các đỉnh của tam giác. Đường tròn này có thể được xác định bằng cách tìm đến các điểm giao giữa các đường bao trùm đỉnh và các đường bao trùm cạnh tam giác. Tâm của đường tròn ngoại tiếp một tam giác chính là giao điểm giữa ba đường trung trực của tam giác. Tâm của đường tròn ngoại tiếp tam giác vuông là trung điểm của cạnh huyền. Ta xét tam giác đều, tâm của đường tròn ngoại tiếp và nội tiếp tam giác sẽ trùng với nhau.

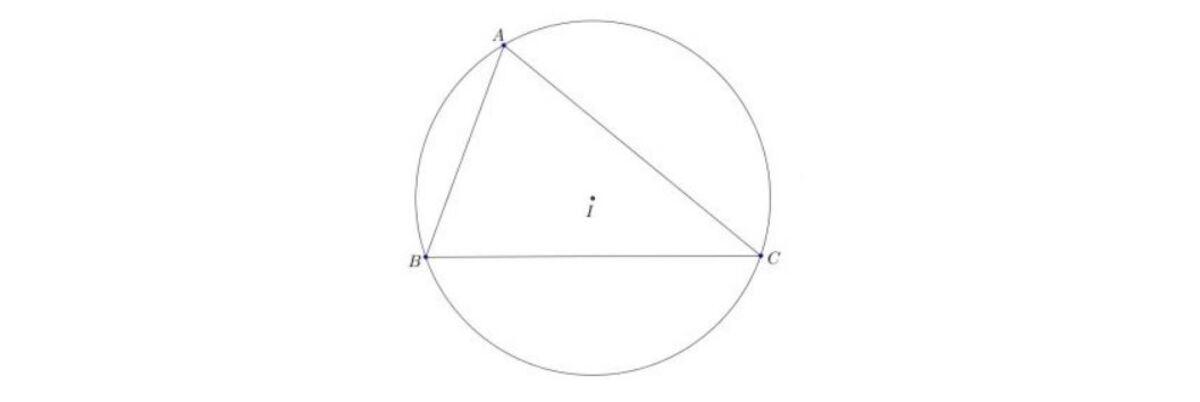
Bài tập về tâm của đường tròn ngoại tiếp tam giác

Dưới đây là một số bài tập về tâm của đường tròn ngoại tiếp tam giác:

1. Tìm tâm của đường tròn ngoại tiếp tam giác ABC với các đỉnh A(2,3), B(-1,1), C(4,0).
2. Chứng minh rằng tâm của đường tròn ngoại tiếp tam giác ABC với các đỉnh A(1,1), B(4,4), C(7,1) nằm trên đường trung trực của tam giác.
3. Tính khoảng cách giữa tâm của đường tròn ngoại tiếp tam giác ABC với đỉnh A khi các đỉnh là A(0,0), B(3,4), C(6,0).
4. Tìm đường tròn ngoại tiếp tam giác với các đỉnh A(2,3), B(-1,1), C(4,0) và chứng minh rằng tâm của đường tròn nằm trên trung điểm của AB.

Những bài tập này giúp bạn củng cố kiến thức về tâm đường tròn ngoại tiếp tam giác và phương pháp tìm tâm, chứng minh, tính toán khoảng cách và các thuật toán liên quan.

Dưới đây là một số bài tập về tâm của đường tròn ngoại tiếp tam giác:

1. Tìm tâm của đường tròn ngoại tiếp tam giác ABC với các đỉnh A(2,3), B(-1,1), C(4,0).
2. Chứng minh rằng tâm của đường tròn ngoại tiếp tam giác ABC với các đỉnh A(1,1), B(4,4), C(7,1) nằm trên đường trung trực của tam giác.
3. Tính khoảng cách giữa tâm của đường tròn ngoại tiếp tam giác ABC với đỉnh A khi các đỉnh là A(0,0), B(3,4), C(6,0).
4. Tìm đường tròn ngoại tiếp tam giác với các đỉnh A(2,3), B(-1,1), C(4,0) và chứng minh rằng tâm của đường tròn nằm trên trung điểm của AB.

Những bài tập này giúp bạn củng cố kiến thức về tâm đường tròn ngoại tiếp tam giác và phương pháp tìm tâm, chứng minh, tính toán khoảng cách và các thuật toán liên quan.

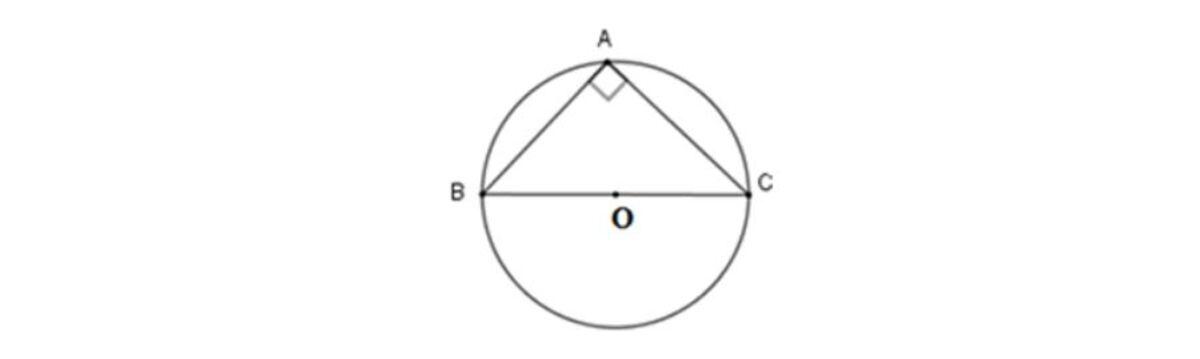
Tâm đường tròn ngoại tiếp tam giác vuông

Tâm đường tròn ngoại tiếp tam giác vuông là một đặc điểm của một tam giác vuông. Nó là điểm giao của ba đường tròn liên tiếp bọc tam giác vuông, với từng cạnh của tam giác vuông. Tâm đường tròn ngoại tiếp này có tên là điểm G (góc) và nó nằm trong phần đường tròn nội tiếp của tam giác.

Ví dụ tâm đường tròn ngoại tiếp tam giác vuông

Ví dụ về tâm đường tròn ngoại tiếp tam giác vuông:

Cho tam giác ABC vuông có cạnh AC là nửa đường chéo của hình chữ nhật. Tìm tâm đường tròn ngoại tiếp của tam giác ABC.

Giải:

• Tìm tọa độ điểm O, tâm đường tròn ngoại tiếp của tam giác ABC.
• Chúng ta biết rằng tâm đường tròn ngoại tiếp của tam giác là giao điểm của 3 đường tròn ngoại tiếp của 3 cạnh tam giác.
• Ta có thể tìm tọa độ điểm O bằng cách sử dụng phương trình đường tròn ngoại tiếp của 3 cạnh tam giác.
• Kết quả cho ta tọa độ điểm O là (A/2, A/2), trong đó A là độ dài cạnh AC của hình chữ nhật.
• Do đó, tâm đường tròn ngoại tiếp của tam giác ABC vuông là điểm O với tọa độ (A/2, A/2).

Tâm đường tròn ngoại tiếp tam giác đều

Tâm đường tròn ngoại tiếp tam giác đều là một điểm trên mặt cầu của tam giác đều, khi mà mỗi đường kẻ từ điểm tâm của đường tròn đến các đỉnh của tam giác đều đều là các góc vuông.

Ví dụ: Tâm đường tròn ngoại tiếp tam giác đều ABC đặt tại điểm O. Chứng minh rằng điểm O là tâm đường tròn ngoại tiếp tam giác đều ABC. Chúng ta có thể sử dụng phép biến đổi giữa độ dài và khoảng cách để chứng minh điều này. Ta có thể biến đổi khoảng cách giữa tâm O và các đỉnh A, B, và C của tam giác ABC thành độ dài đoạn thẳng gọi là các cạnh trung tuyền. Chúng ta sẽ chứng minh rằng các cạnh trung tuyền của tam giác đều ABC đều nằm trên đường tròn ngoại tiếp tâm O.

Ví dụ tâm đường tròn ngoại tiếp tam giác đều

Ví dụ về tâm đường tròn ngoại tiếp tam giác đều có thể là tam giác ABC có 3 cạnh đều. Nếu gọi O là tâm đường tròn ngoại tiếp tam giác, thì O sẽ nằm trên giao điểm của 3 đường trung tuyến của tam giác ABC. Để chứng minh điều này, ta cần sử dụng một số chứng minh về hình học.

Cụ thể hơn, nếu ta gọi I là giữa của cạnh AB, J là giữa của cạnh BC, và K là giữa của cạnh AC. Ta có thể chứng minh rằng AI, BJ, CK đều cân bằng với nhau và có độ dài bằng nửa độ dài của cạnh tương ứng của tam giác ABC. Từ đó, ta có thể chứng minh rằng O nằm trên giao điểm của đường trung tuyến AI, BJ, CK.

Vậy, tâm đường tròn ngoại tiếp tam giác đều là một điểm đặc biệt trên tam giác, đặc biệt là nằm trên giao điểm của 3 đường trung tuyến của tam giác.

Tâm đường tròn ngoại tiếp tam giác cân

Tâm đường tròn ngoại tiếp tam giác cân là điểm cực tiểu của đường tròn ngoại tiếp tam giác cân. Nếu tam giác ABC cân, thì điểm này sẽ là trung điểm của đoạn BC, và nằm trên đường trung trực của đoạn AB.

Ví dụ tâm đường tròn ngoại tiếp tam giác cân

Một ví dụ về tâm đường tròn ngoại tiếp tam giác cân là tam giác ABC có các đỉnh A, B, và C. Ta kết nối các đỉnh với tâm O của đường tròn ngoại tiếp. Nếu độ dài các cạnh AB, BC, và AC bằng nhau, thì ta có một tam giác cân và tâm O của đường tròn ngoại tiếp sẽ nằm trên đường trung tuyến của tam giác.

Chứng minh rằng tâm đường tròn ngoại tiếp tam giác cân là giữa đường trung tuyến của tam giác có thể được thực hiện bằng cách sử dụng các thủ thuật toán học về tam giác và đường tròn.

Tâm đường tròn ngoại tiếp tam giác vuông nằm ở

Tâm đường tròn ngoại tiếp tam giác vuông nằm trên gốc tọa độ của đường tròn, chính giữa các đỉnh của tam giác và vuông góc với gốc tọa độ.

Cách xác định tâm đường tròn ngoại tiếp tam giác

Có một số cách xác định tâm đường tròn ngoại tiếp tam giác, trong đó có:

1. Xác định tâm đường tròn ngoại tiếp tam giác bằng phương pháp giữa.
2. Xác định tâm đường tròn ngoại tiếp tam giác bằng phương pháp đồ thị.
3. Xác định tâm đường tròn ngoại tiếp tam giác bằng phương pháp toán học.

Ngoài ra, bạn có thể sử dụng phần mềm hoặc các công cụ khác để xác định vị trí chính xác của tâm đường tròn ngoại tiếp tam giác.

1. Đường tròn ngoại tiếp tam giác là gì?

Đường tròn ngoại tiếp của tam giác là đường tròn đi qua các đi qua tất cả các đỉnh của tam giác đó. Tâm của đường tròn ngoại tiếp là giao điểm của ba đường trung trực của tam giác đó.

2. Tâm đường tròn ngoại tiếp là gì?

Giao của 3 đường trung trực trong tam giác là tâm đường tròn ngoại tiếp (hoặc có thể là 2 đường trung trực).

3. Tính chất đường tròn ngoại tiếp

– Mỗi tam giác chỉ có 1 đường tròn ngoại tiếp.

– Tâm của đường tròn ngoại tiếp tam giác là giao điểm giữa 3 đường trung trực của tam giác.

– Tâm của đường tròn ngoại tiếp tam giác vuông là trung điểm của cạnh huyền.

– Đối với tam giác đều, tâm đường tròn ngoại tiếp và nội tiếp tam giác trùng với nhau.

4. Các công thức tính bán kính đường tròn ngoại tiếp

Công thức tính bán kính đường tròn ngoại tiếp tam giác bằng tích của 3 cạnh tam giác chia bốn lần diện tích:

5. Cách xác định tâm đường tròn ngoại tiếp tam giác

Xác định tâm của đường tròn ngoại tiếp tứ giác

+ Tứ giác có bốn đỉnh các đều một điểm. Điểm đó là tâm đường tròn ngoại tiếp tam giác

+ Lưu ý: Quỹ tích các điểm nhìn đoạn thẳng AB dưới một góc vuông là đường tròn đường kính AB

– Có 2 cách để xác định tâm đường tròn ngoại tiếp tam giác như sau:

– Cách 1

+ Bước 1: Gọi I(x;y) là tâm của đường tròn ngoại tiếp tam giác ABC. Ta có IA=IB=IC=R

+ Bước 2: Tọa độ tâm I là nghiệm của hệ phương trình

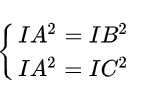 – Cách 2:

+ Bước 1: Viết phương trình đường trung trực của hai cạnh bất kỳ trong tam giác.

+ Bước 2: Tìm giao điểm của hai đường trung trực này, đó chính là tâm của đường tròn ngoại tiếp tam giác.

– Như vậy Tâm của đường tròn ngoại tiếp tam giác ABC cân tại A nằm trên đường cao AH

Tâm của đường tròn ngoại tiếp tam giác vuông là trung điểm cạnh huyền

Để giải được bài toán viết phương trình đường tròn ngoại tiếp tam giác ta thực hiện theo 4 bước sau:

+ Bước 1: Thay tọa độ mỗi đỉnh vào phương trình với ẩn a,b,c (Bởi các đỉnh thuộc đường tròn ngoại tiếp, nên tọa độ các đỉnh thỏa mãn phương trình đường tròn ngoại tiếp cần tìm)

+ Bước 2: Giải hệ phương trình tìm a,b,c

+ Bước 3: Thay giá trị a,b,c tìm được vào phương trình tổng quát ban đầu => phương trình đường tròn ngoại tiếp tam giác cần tìm.

+ Bước 4: Do A,B,C ∈ C nên ta có hệ phương trình:

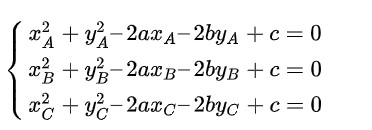
=> Giải hệ phương trình trên ta tìm được a, b, c.

Thay a, b, c vừa tìm được vào phương trình (C) ta có phương trình đường tròn ngoại tiếp tam giác cần tìm.

7. Bán kính đường tròn ngoại tiếp tam giác

Cho tam giác ABC

Gọi a, b, c lần lượt là độ dài các cạnh BC, AC, AB. S là diện tích tam giác ABC

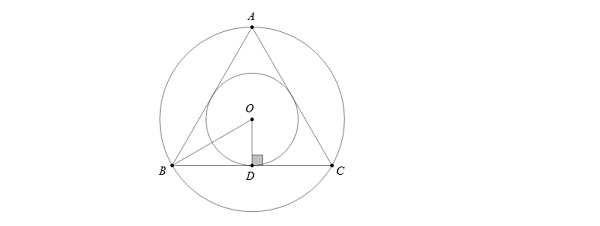
Ta có bán kính đường tròn nội tiếp tam giác ABC là:

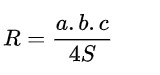
8. Bài tập về đường tròn ngoại tiếp tam giác

Dạng 1: Viết phương trình đường tròn nội tiếp tam giác ABC khi biết tọa độ 3 đỉnh

VD: Viết phương trình đường tròn ngoại tiếp tam giác A, B, C biết A(-1;2) B(6;1) C(-2;5)

Cách giải:

Gọi phương trình đường tròn ngoại tiếp tam giác ABC có dạng:

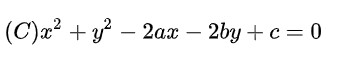
Do A, B, C cùng thuộc đường tròn nên thay tọa độ A, B, C lần lượt vào phương trình đường tròn (C) ta được hệ phương trình:

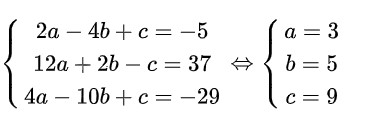
Do đó, Phương trình đường tròn ngoại tiếp tam giác ABC tâm I (3;5) bán kính R = 5 là:

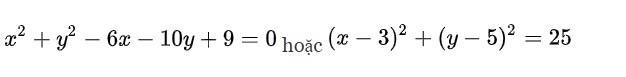
Dạng 2: Tìm tâm của đường tròn ngoại tiếp khi biết tọa độ ba đỉnh

Ví dụ: Cho tam giác ABC với A(1;2), B(-1;0), C(3;2). Tìm tọa độ tâm của đường tròn ngoại tiếp tam giác ABC

Hướng dẫn cách giảiGọi I(x;y) là tâm của đường tròn ngoại tiếp tam giác ABC

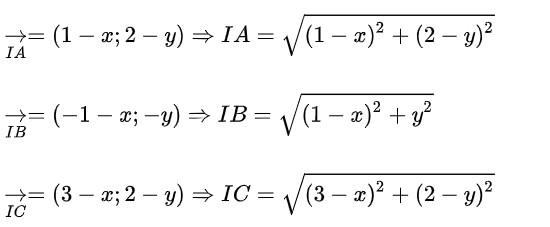
Vì I là tâm của đường tròn ngoại tiếp tam giác ABC nên ta có:

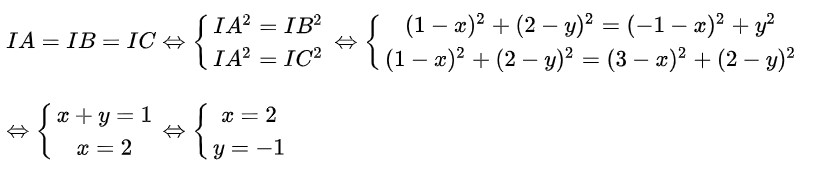
Vậy tọa độ tâm của đường tròn ngoại tiếp tam giác ABC là I(2;-1)

Dạng 3: Tìm bán kính đường tròn nội tiếp tam giác

VD: Tam giác ABC có cạnh AB = 3, AC = 7, BC = 8. Tính bán kính đường tròn ngoại tiếp tam giác ABC

Cách giải:

Ta có:

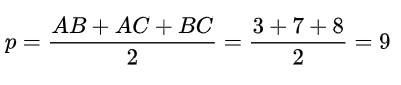Áp dụng công thức Herong:

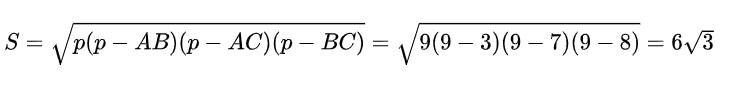
Bán kính đường tròn ngoại tiếp tam giác ABC:

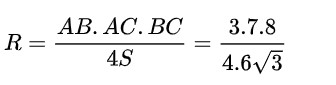
VD 4: Cho tam giác MNP vuông tại N, và MN = 6cm, NP = 8cm. Xác định bán kính đường tròn ngoại tiếp tam giác MNP bằng bao nhiêu?

Cách giải:

Áp dụng định lý Pytago ta có:

PQ = 1/2 MP => NQ = QM = QP = 5cm.

Gọi D là trung điểm MP => ∆MNP vuông tại N có NQ là đường trung tuyến ứng với cạnh huyền MP.

=> Q là tâm đường tròn ngoại tiếp ∆MNP.

Suy ra: Đường tròn ngoại tiếp ∆MNP có tâm Q của cạnh huyền MP và bán kính R = MQ = 5cm.

VD 5: Cho tam giác ABC đều với cạnh bằng 6cm. Xác định tâm và bán kính của đường tròn ngoại tiếp tam giác ABC?

Cách giải

Gọi D, E lần lượt là trung điểm của cạnh BC, AB và AD giao với CE tại O

Ta có: Tam giác ABC đều => Đường trung tuyến cũng là đường cao, đường phân giác, đường trung trực của tam giác.

Suy ra: O là tâm đường tròn ngoại tiếp tam giác.

∆ABC có CE là đường trung tuyến => CE cũng là đường cao.

Áp dụng định lí Pytago vào tam giác vuông AEC có:

CE² = AC² – AE² = 6² – 3² = 27 => CE =3√3cm.

Ta có: O là trọng tâm của tam giác ABC => CO = 2/3 CE = (2/3)3√3 = 2√3cm.

Suy ra: Tâm đường tròn ngoại tiếp tam giác ABC là trọng tâm O và bán kính là OC = 2√3cm.

VD5: Cho tam giác MNP vuông tại N, và MN=6 cm, N P=8 cm,. Xác định bán kính đường tròn ngoại tiếp tam giác MNP bằng bao nhiêu?

Giải:

Đáp án bài tập 1

Áp dụng định lý Pytago ta có:

PQ = 1/2MP => NQ = QM = QP = 5cm

Gọi D là trung điểm  MP => △MNP vuông tại N có NQ là đường trung tuyến ứng với cạnh huyền  MP=> Q là tâm đường tròn ngoại tiếp △MNP

Suy ra: Đường tròn ngoại tiếp △MNP có tâm Q của cạnh huyền MP và bán kính R = MQ = 5cm

9. Bài tập tâm đường tròn ngoại tiếp tam giác

Bài 1: Các đường cao AD, BE của tam giác ABC cắt nhau tại H (góc C khác góc vuông) và cắt đường tròn (O) ngoại tiếp tam giác ABC lần lượt tại I và K.

a, Chứng minh tứ giác CDHE nội tiếp và xác định tâm của đường tròn ngoại tiếp tứ giác đó

b, Chứng minh tam giác CIK là tam giác cân

Bài 2: Cho tam giác ABC có ba góc nhọn nội tiếp trong đường tròn (O; R). Ba đường của tam giác là AF, BE và CD cắt nhau tại H. Chứng minh tứ giác BDEC là tứ giác nội tiếp. Xác định tâm I của đường tròn ngoại tiếp tứ giác

Bài 3: Cho tam giác ABC vuông tại A có AB Bài 4: 

Cho tam giác ABC cân tại A, AB = AC nội tiếp đường tròn tâm O. Các đường cao AQ, BE, CF cắt nhau tại một điểm.

a, Chứng minh rằng tứ giác AEHF là tứ giác nội tiếp, xác định tâm của đường tròn ngoại tiếp tứ giác đó

b, Cho bán kính đường tròn tâm I là 2cm góc BAC = 50⁰. Tính độ dài cung EHF của đường tròn tâm I và diện tích hình quạt tròn IEHF