Bạn đang xem bài viết Tính chất hình thang là gì? Tìm hiểu kiến thức hình thang tại Thcslytutrongst.edu.vn bạn có thể truy cập nhanh thông tin cần thiết tại phần mục lục bài viết phía dưới.
Hình thang là một hình học phổ biến và quen thuộc trong lĩnh vực toán học. Được tạo thành từ bốn đỉnh và bốn cạnh, hình thang không chỉ đẹp mắt mà còn mang trong mình những tính chất đặc biệt. Việc tìm hiểu về kiến thức liên quan đến hình thang không chỉ giúp chúng ta hiểu rõ hơn về cấu trúc và tính chất của nó mà còn cung cấp cho chúng ta một cách tiếp cận mới để giải quyết những bài toán hình học phức tạp. Trong bài viết này, chúng ta sẽ khám phá những khía cạnh đặc trưng của hình thang, từ các định nghĩa cơ bản, các định lý quan trọng cho đến các ví dụ và ứng dụng thực tế.
Các tính chất hình thang được sử dụng khá nhiều trong các bài tập hình học. Bài viết sau của Chúng Tôi sẽ giúp bạn ôn tập lại toàn bộ những kiến thức liên quan đến hình thang. Mời bạn đọc theo dõi bài viết dưới đây của Chúng Tôi để biết rõ hơn nhé!
Hình thang là gì?
Hình thang là gì?
Hình thang là gì luôn là câu hỏi mà các bạn học sinh thắc mắc, nội dung sau của Chúng Tôi sẽ giải đáp định nghĩa và tính chất hình thang.
Hình thang là một tứ giác lồi có hai cạnh đối song song. Hai cạnh này được gọi là hai cạnh đáy của hình thang. Hai cạnh còn lại được gọi là hai cạnh bên.
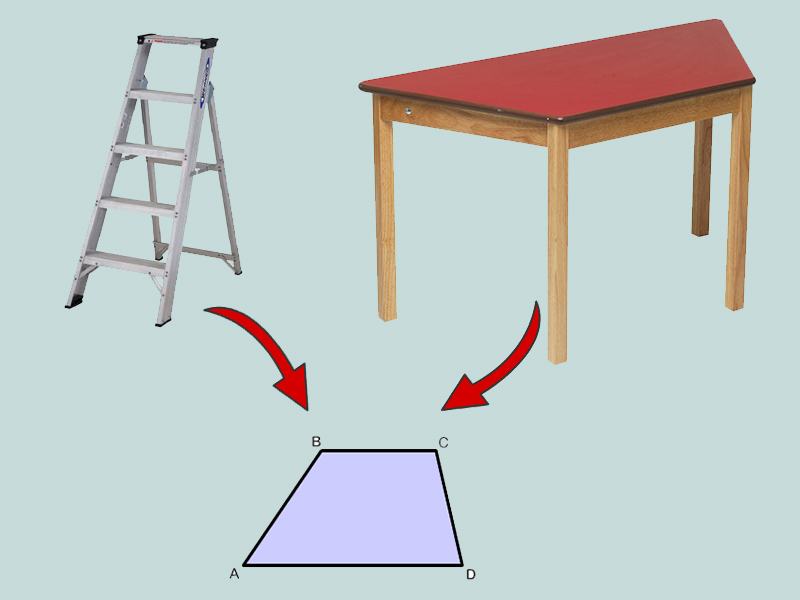
Dấu hiệu nhận biết hình thang
Dưới đây là một số dấu hiệu nhận biết của hình thang mà Chúng Tôi đã tổng hợp được. Mời bạn đọc cùng tham khảo:
- Tứ giác có hai cạnh đối song song gọi là hình thang.
- Hình thang có một góc vuông gọi là hình thang vuông.
- Hình thang có hai góc kề một đáy gọi là hình thang cân.
- Hình thang có hai cạnh bên bằng nhau gọi là hình thang cân.
- Hình thang có hai đường chéo bằng nhau gọi là hình thang cân.
Vừa rồi là những dấu hiệu nhận biết hình thang. Tiếp theo bài viết là phần nội dung chính về tính chất hình thang. Theo dõi cùng Chúng Tôi nhé!
Tính chất hình thang
Tính chất hình thang được phân các nội dung, bao gồm tính chất về góc, tính chất về cạnh và tính chất đường trung bình.
Tính chất về góc
Tính chất về góc của hình thang là hai góc kề một cạnh bên của hình thang có tổng bằng 180°. Hai góc này nằm ở vị trí trong cùng phía của hai đoạn thẳng song song là 2 cạnh đáy. Riêng đối với hình thang cân, hai góc kề một đáy bằng nhau.
Tính chất về cạnh
Sau đây là 3 tính chất về cạnh, mời bạn đọc cùng tham khảo:
- Nếu một hình thang có hai cạnh đáy bằng nhau thì hai cạnh bên song song và bằng nhau.
- Ngược lại, nếu một hình thang có hai cạnh bên song song thì chúng bằng nhau và hai cạnh đáy cũng bằng nhau.
- Trong hình thang cân, hai đường chéo bằng nhau.
Định nghĩa, tính chất đường trung bình
Nói đến tính chất hình thang không thể không kể đến định nghĩa và tính chất đường trung bình của hình thang. Đường trung bình của hình thang là đường thẳng nối trung điểm hai cạnh bên của hình thang. Đường trung bình của hình thang có độ dài bằng nửa tổng độ dài hai cạnh đáy.
Chắc hẳn qua một số nội dung mà Chúng Tôi cung cấp, bạn cũng phần nào biết được tính chất hình thang. Tiếp theo bài viết là phần thông tin về các dạng đặc biệt của hình thang. Mời độc giả cùng theo dõi.
Các dạng đặc biệt của hình thang
Hình thang vuông
Hình thang vuông là hình thang có một góc vuông. Tính chất hình thang vuông là có hai góc vuông. Đây là kiến thức khá cơ bản bạn cần nhớ để biết áp dụng vào bài tập sao cho phù hợp.
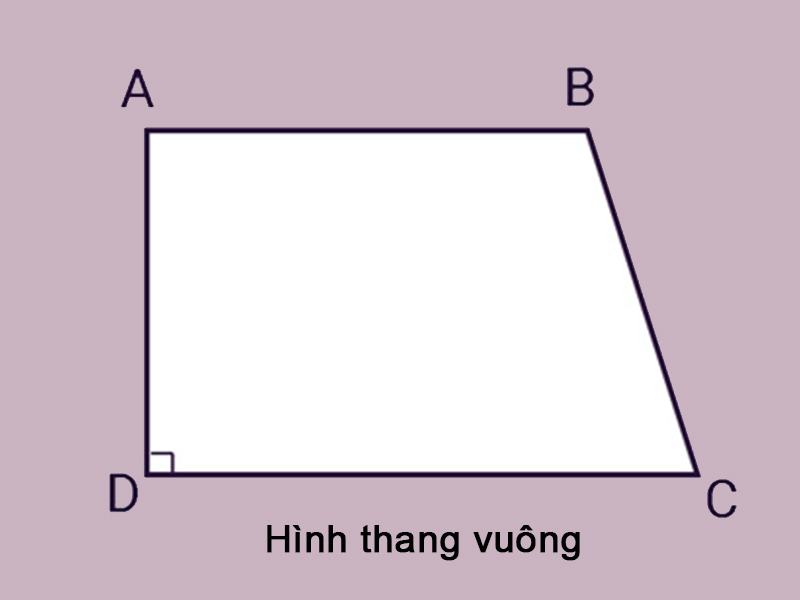
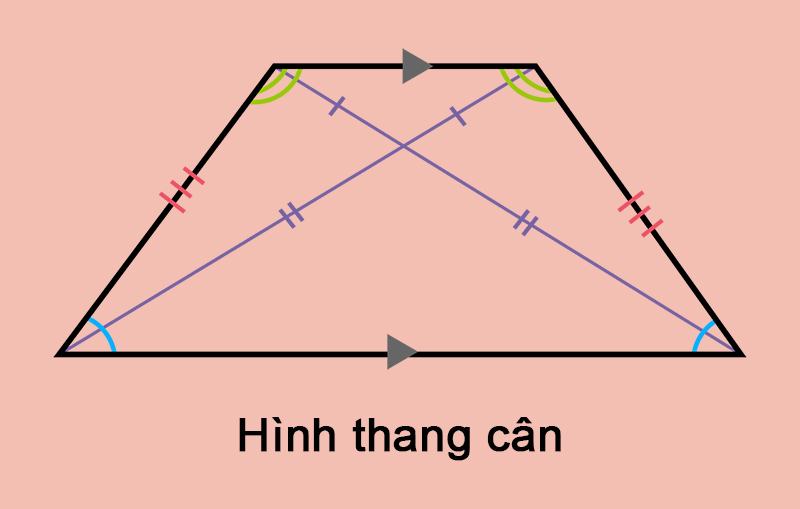
Hình thang cân
Hình thang cân là hình thang có hai góc kề một đáy bằng nhau. Bạn nên nhớ kiến thức này để hoàn thành bài tập một cách tốt nhất nhé!
Sau đây là một số tính chất hình thang cân:
- Hai cạnh bên bằng nhau.
- Hai góc kề cạnh đáy bằng nhau.
- Hai đường chéo bằng nhau.
- Hình thang cân nội tiếp đường tròn.
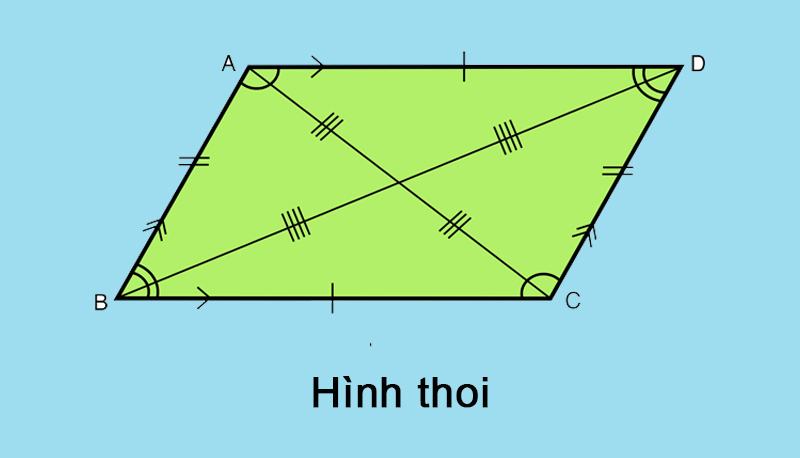
Hình bình hành
Hình bình hành là một dạng đặc biệt của hình thang, mời bạn đọc theo dõi nội dung sau để khám phá nó nhé! Hình thang có 2 cạnh đáy bằng nhau, 2 cạnh bên song song và bằng nhau được gọi là hình bình hành.
Dưới đây là một số tính chất của hình bình hành:
- Các cạnh đối song song và bằng nhau.
- Các góc đối bằng nhau.
- Hai đường chéo cắt nhau tại trung điểm của mỗi đường.
Hình chữ nhật
Hãy cùng Chúng Tôi tìm hiểu về định nghĩa và tính chất của hình chữ nhật nhé!
Hình chữ nhật là hình thang vừa vuông vừa cân.
Dưới đây là các tính chất về hình chữ nhật mà bạn nên biết:
- Trong hình chữ nhật, hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường.
- Các đường chéo cắt nhau tạo thành 4 tam giác cân.
- 4 góc vuông bằng nhau.
- Các cạnh đối song song và bằng nhau.

Các công thức về hình thang
Công thức tính diện tích hình thang
Sau khi biết được tính chất hình thang, Chúng Tôi sẽ bật mí giúp bạn các công thức tính diện tích hình thang. Hãy theo dõi nội dung dưới đây để biết rõ hơn nhé!
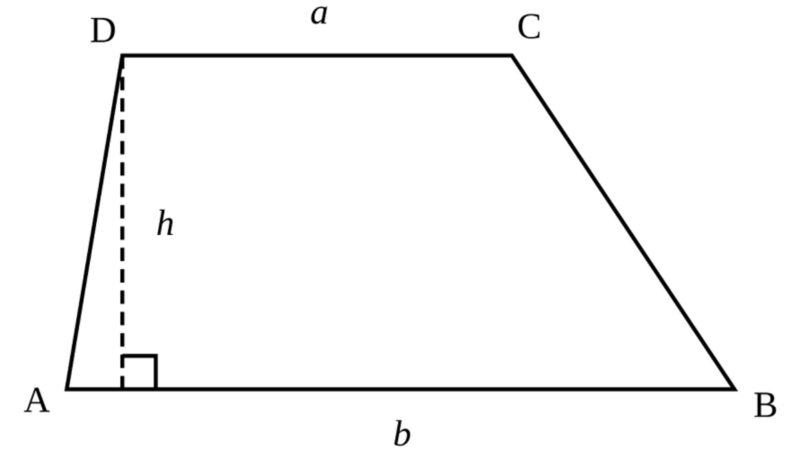
Công thức diện tích hình thang: S = h x ((a +b)/2)
Trong đó:
- S: Diện tích.
- a, b: Lần lượt là độ dài 2 đáy.
- h: Chiều cao hình thang.
Công thức tính chu vi hình thang
Sau đây là công thức tính chu vi mà bạn cần nên nhớ để áp dụng vào bài tập. Mời các bạn cùng tham khảo.
Công thức: P = a + b + c + d.
Trong đó:
- P: Chu vi hình thang.
- a, b: Lần lượt là độ dài 2 cạnh đáy.
- c, d: Lần lượt là độ dài 2 cạnh bên.
Các dạng bài tập thông dụng về tính chất hình thang
Dưới đây là các dạng bài tập thông dụng về tính chất hình thang mà Chúng Tôi đã tổng hợp được. Mời bạn đọc cùng theo dõi.
Đề bài 1: Cho hình thang ABCD (AB//CD), biết góc A – góc D = 20o, góc B = 2 góc C. Yêu cầu tính các góc của hình thang.
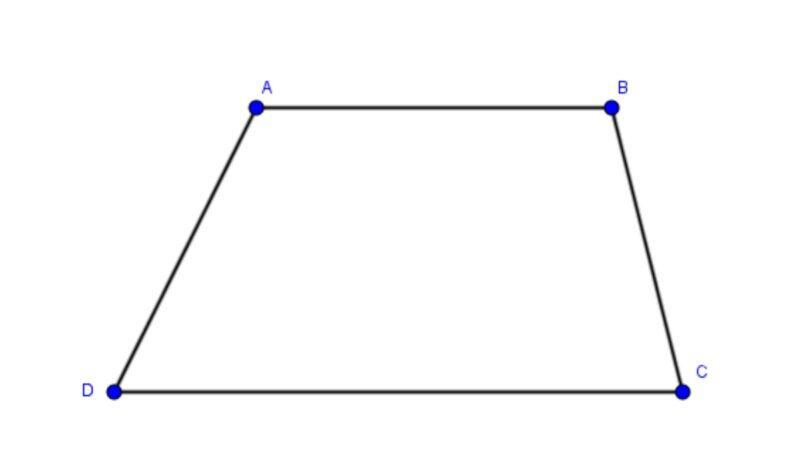
Đáp án:
Theo giả thiết ta có: Góc A – góc D = 20o, góc A + góc D = 180o (hai góc trong cùng phía). (1)
Góc A – góc D = 20o => Góc A = Góc D + 20o. (2)
Thay (2) vào (1) ta được:
Góc A + góc D = Góc D + 20o + góc D = 2 góc D + 20o = 180o
- Góc D = (180o – 20o)/2 = 80o.
Thay góc D = 80o vào góc A ta được 20o + 80o = 100o.
Ta lại có: Góc B = 2 góc C. (3)
Góc B + góc C = 180o. (hai góc trong cùng phía bù nhau) (4)
Thay (3) vào (4) ta được: 2 góc C + góc C = 180o hay 3 góc C = 180o => Góc C = 60o.
Do đó: Góc B = 2 góc C = 2 * 60o = 120o.
Đề bài 2: Cho hình thang ABCD có đáy lớn AB. Gọi M, N, P, Q lần lượt là trung điểm của đoạn thẳng AD, BC, AC, BD. Yêu cầu:
Câu 1: Chứng minh bốn điểm M, N, P, Q nằm trên cùng một đường thẳng.
Câu 2: Cho AB = a, CD = b (với a > b). Tính độ dài các đoạn MN, PQ.
Câu 3: Chứng minh nếu MP = PQ = QN thì a – 2b = 0.
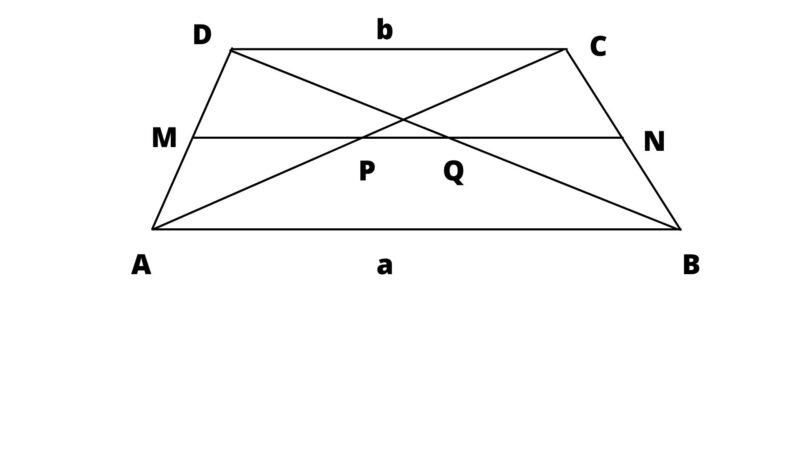
Đáp án:
Câu 1: Nhìn hình ta có thể thấy: MP//DC và MQ//AB.
Kết hợp với AB//DC suy ra MP MQ
=> Ba điểm M, P, Q thẳng hàng
Tương tự, 3 điểm N, P, Q thẳng hàng
Suy ra 4 điểm M, N, P, Q nằm trên cùng một đường thẳng.
Câu 2: Ta có MN là đường trung bình của hình thang ABCD
Suy ra: MN = ½ (a+b)
Mặt khác ta có:
MQ = ½ AB =½ a;
MP = ½ DC = ½ b;
PQ = MQ – MP = ½ (a-b)
Câu 3: Khi MP = PQ = QN => ⅓ MN = PQ
Suy ra ⅙ (a+b) = ½ (a-b)
=> (a+b) = 3(a-b) => a = 2b.
Đề bài 3: Cho hình thang ABCD, đáy AB = 40 (đvđd), CD = 80 (đvđd), cạnh bên BC = 50 (đvđd) và AD = 30 (đvđd). Yêu cầu: Chứng minh ABCD là hình thang vuông.
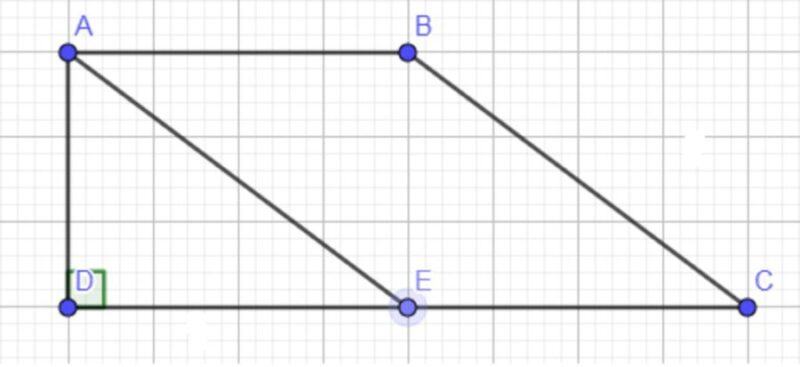
Đáp án:
Từ đỉnh A kẻ đường thẳng song song với BC và cắt DC tại E.
Ta có: AE = BC = 50 (đvđd); EC = AB = 40 (đvđd)
=> DE = 80 – 40 = 40 (đvđd)
Tam giác ADE có AD = 30 (đvđd), DE = 40 (đvđd) và AE = 50 (đvđd)
Nên: AD2 = 302 = 900; DE2 = 402 = 1600; AE2 = 502 = 25000
- AE2 = AD2 + DE2 (Theo định lý Pytago cho tam giác vuông ADE)
Suy ra: Góc A = Góc D = 90o
- Tứ giác ABCD là hình thang vuông (đpcm).
Vừa rồi là những kiến thức liên quan đến hình thang, chẳng hạn như tính chất hình thang, công thức hình thang,… Hi vọng những thông tin này sẽ giúp ích cho việc học tập môn Toán của bạn. Hẹn gặp bạn đọc trong những bài viết tiếp theo của Chúng Tôi.
Tính chất hình thang là những đặc điểm độc đáo và quan trọng của hình thang trong hình học. Để tìm hiểu kiến thức về hình thang, chúng ta cần biết rõ những tính chất này.
Tính chất đầu tiên của hình thang là sự đối xứng về đường chéo. Trong một hình thang, đường chéo chia hình tỷ lệ bằng nhau và cắt qua nhau tại một điểm. Điều này đồng nghĩa với việc đường chéo làm cho hai tam giác bên trong hình thang có cả hai cặp cạnh tương tự.
Tính chất thứ hai của hình thang là các góc đối diện bằng nhau. Hai cặp góc đối diện của một hình thang có giá trị bằng nhau. Điều này được gọi là tính chất góc đối diện của hình thang, và nó có thể được chứng minh bằng cách sử dụng các định lý về góc đồng quy.
Tính chất tiếp theo là tâm của hai đường cao của một hình thang nằm trên đường chéo chung. Điều này có nghĩa là khi vẽ hai đường cao từ các đỉnh đối diện của hình thang, chúng sẽ cắt nhau tại một điểm trên đường chéo chung của hình thang.
Cuối cùng, tính chất cuối cùng của hình thang là tổng độ dài hai bên đáy bằng tổng độ dài hai cạnh bên. Điều này được gọi là định lý hình thang, và nó có thể được chứng minh bằng cách sử dụng định lý Pythagoras hoặc áp dụng các công thức trội khác trong hình học.
Tóm lại, tính chất hình thang là những điểm độc đáo và quan trọng mà ta cần biết khi nghiên cứu về hình thang. Các tính chất này giúp chúng ta hiểu rõ hơn về cấu trúc và đặc điểm của hình thang, từ đó áp dụng vào các bài toán và vấn đề liên quan trong hình học và các lĩnh vực khác.
Cảm ơn bạn đã xem bài viết Tính chất hình thang là gì? Tìm hiểu kiến thức hình thang tại Thcslytutrongst.edu.vn bạn có thể bình luận, xem thêm các bài viết liên quan ở phía dưới và mong rằng sẽ giúp ích cho bạn những thông tin thú vị.
Từ Khoá Liên Quan:
1. Hình thang
2. Đường chéo hình thang
3. Cạnh bên hình thang
4. Hai góc đáy hình thang
5. Hai góc đỉnh hình thang
6. Công thức tính diện tích hình thang
7. Công thức tính chu vi hình thang
8. Hình thang cân
9. Hình thang vuông
10. Hình thang nghiêng
11. Hình thang lồi
12. Hình thang lõm
13. Hình thang có đỉnh nằm ngoài đoạn thẳng nối hai đỉnh đáy
14. Hình thang có đỉnh nằm trong đoạn thẳng nối hai đỉnh đáy
15. Hình thang chứa hình tam giác


