Bạn đang xem bài viết Tính chất kết hợp của phép cộng? Lời giải bài tập trong SGK tại Thcslytutrongst.edu.vn bạn có thể truy cập nhanh thông tin cần thiết tại phần mục lục bài viết phía dưới.
Phép cộng là một phép toán rất quan trọng trong toán học và được sử dụng hàng ngày trong cuộc sống. Phép cộng có tính chất kết hợp, tức là kết quả của việc cộng ba số không phụ thuộc vào cách thực hiện phép cộng. Trong bài viết này, chúng ta sẽ đi vào tìm hiểu về tính chất kết hợp của phép cộng và cách chứng minh tính chất này.
Theo sách giáo khoa, tính chất kết hợp của phép cộng được định nghĩa như sau: “Với mọi số nguyên a, b và c, ta có (a + b) + c = a + (b + c)”. Đơn giản hơn, tính chất này nói rằng việc thay đổi thứ tự của các số trong phép cộng không ảnh hưởng đến kết quả cuối cùng.
Để chứng minh tính chất kết hợp, ta có thể sử dụng phương pháp chứng minh bằng quy nạp. Quy nạp là một phương pháp chứng minh toán học dựa trên nguyên tắc xác định một câu đúng cho một giá trị cơ sở, sau đó chứng minh câu đúng đó sẽ kéo theo câu đúng cho giá trị tiếp theo, và tiếp tục cho tới khi chứng minh được câu đúng cho tất cả các giá trị.
Dưới đây là lời giải bài tập trong sách giáo khoa về tính chất kết hợp của phép cộng:
Ta giả sử a, b và c là ba số nguyên bất kỳ.
Theo tính chất kết hợp của phép cộng, ta cần chứng minh rằng (a + b) + c = a + (b + c).
Ta thực hiện chứng minh bằng quy nạp.
Với trường hợp cơ sở, ta thử với a = 1, b = 2 và c = 3.
Ta có (1 + 2) + 3 = 3 + 3 = 6;
và a + (b + c) = 1 + (2 + 3) = 1 + 5 = 6.
Kết quả của cả hai phép tính là 6, không phụ thuộc vào thứ tự của các số.
Giả sử tính chất kết hợp đúng với a, b và c.
Ta cần chứng minh rằng tính chất này cũng đúng với a + 1, b + 1 và c + 1.
Ta có ((a + 1) + (b + 1)) + (c + 1) = (a + (1 + (b + 1))) + (c + 1)
= ((a + (b + 1)) + 1) + (c + 1)
= (((a + b) + 1) + 1) + (c + 1)
= (a + b) + ((1 + 1) + (c + 1))
= (a + b) + ((c + 1) + 2)
= (a + b) + (c + (1 + 2))
= a + (b + (c + 3))
= a + ((b + c) + 3)
= (a + (b + c)) + 3
= (a + b) + (c + 3)
= a + (b + (c + 3))
= a + ((b + c) + 3).
Vậy, ta kết luận tính chất kết hợp của phép cộng đúng với mọi số nguyên a, b và c.
Qua bài viết trên, chúng ta đã đi vào tìm hiểu về tính chất kết hợp của phép cộng và cách chứng minh tính chất này qua một ví dụ cụ thể. Tính chất kết hợp của phép cộng là một điều cơ bản trong toán học và rất hữu ích trong việc giải quyết các bài toán liên quan đến phép cộng.
Chúng Tôi sẽ giới thiệu toán lớp 4 tính chất kết hợp của phép cộng đến với các em học sinh và phụ huynh. Đây là một trong những tính chất quan trọng của phép cộng, có thể áp dụng vào các bài toán để tìm ra đáp án nhanh hơn nhé!
Tính chất kết hợp của phép cộng là gì?
Tính chất kết hợp của phép cộng
Tính chất kết hợp của phép cộng là khi cộng một tổng hai số với số thứ ba, ta có thể cộng số thứ nhất với tổng của số thứ hai và số thứ ba.
Công thức như sau: (a + b) + c= a + (b + c).

So sánh giá trị của hai biểu thức (a + b) + c và a + (b + c)
So sánh giá trị của hai biểu thức (a + b) + c và a + (b + c) trong bảng sau:
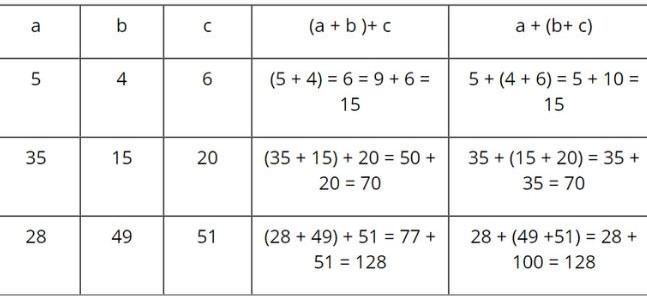
Qua bảng ở trên, ta thấy giá trị của (a +b) + c và của a + (b + c) luôn luôn bằng nhau.
Chú ý: Ta có thể tính giá trị của biểu thức dạng a + b + c như sau:
a + b + c = (a + b) + c = a + (b + c)
Chủ đề liên quan:
- Tính chất chia hết của một tổng? Các dạng bài tập cần biết
- Tính chất cơ bản của phân số – Một số bài toán lớp 6
Bài tập vận dụng tính chất kết hợp của phép cộng
Bài tập vận dụng
Câu 1: Tính
a ) 5264 + 3978 + 4736.
b ) 42716 + 37284 +6767.
Câu 2: Tính bằng cách thuận tiện nhất :
a ) 81 + 35 + 19.
b ) 78 +65 + 135 + 22.
Câu 3. Một xã tổ chức tiêm phòng bệnh cho trẻ em. Lần đầu có 1465 em tiêm phòng bệnh, lần sau có nhiều hơn lần đầu 335 em tiêm phòng bệnh. Hỏi cả hai lần có bao nhiêu em đã tiêm phòng bệnh ?
Hướng dẫn
Câu 1: Sử dụng tính chất kết hợp của phép cộng để nhóm những số hàng có tổng là số tròn trăm, tròn nghìn với nhau Từ đó, tính tổng sẽ nhanh và chính xác hơn.
a) 5264 + 3978 + 4736 = (5264 + 4736) + 3978
= 10 000 + 3978 = 13 978
b) 42716 + 37284 +6767 = (42716 + 37284) + 6767
=80000 + 6767 = 86767
Câu 2: Sử dụng tính chất kết hợp của phép cộng để nhóm những số hàng có tổng là số tròn trăm, tròn nghìn với nhau. Từ đó, tính tổng sẽ nhanh và chính xác hơn.
a) 81 + 35 + 19 = (81 + 19) + 35
= 100 + 35
= 135
b) 78 +65 + 135 + 22 = (78 + 22) + (65 + 135)
= 100 + 200
= 300
Câu 3: Đầu tiên chúng ta tính số em tiêm phòng lần thứ 2 trước, sau đó cộng kết quả đó với số trẻ em tiêm phòng lần 1 mà đề bài đã cho sẽ ra được kết quả.
Số em tiêm phòng bệnh lần thứ hai là: 1465 + 335 = 1800 (em).
Số em tiêm phòng bệnh cả hai lần là: 1465 + 1800 = 3265 (em).
Đáp số: 3265 (em).
Bài tập tự luyện tính chất kết hợp của phép cộng
Câu 1: Tính bằng cách thuận tiện nhất:
a) 72 + 9 + 8.
b) 37 + 18 + 3.
c) 48 + 26 + 4.
d) 85 + 99 +1.
e) 67 +98 + 33.
f) 25 + 19 + 5.
Câu 2. Tính nhanh:
a) 145 +86 + 14 +55.
b) 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9.
c) 34000 + 57859 + 66000.
d) 8973 + 45783 + 46027 + 54217.
Câu 3: Một hình chữ nhật có chiều dài là a, chiều rộng là b ( a , b cùng một đơn vị đo ). Gọi P là chu vi , S là diện tích của hình chữ nhật . Ta có:
P = (a + b) x 2 và S = a x b.
Viết vào ô trống (theo mẫu): P = (a + b)x 2S = a x b.
a: 6cm, 24cm, 9cm.
b: 3cm, 6cm, 9cm.
Đáp án
Câu 2:
a) 89.
b)58.
c) 78.
d) 185.
e) 198.
f) 49.
Câu 2:
a) 300.
b) 45.
c) 157859.
d) 155000.
Câu 3:
P = (a + b)x 2.
a: 6cm b: 3cm P = (6 + 3) x 2 = 36 cm), S = 6 x 3 = 18 (cm2).
a: 24cm b: 6cm P = (24 + 6) x 2 = 60 (cm), S= 24 x 6 = 144 (cm2).
a: 9cm b: 9cm P = (9 +9) x 2 = 36 (cm), S = 9 x 9 = 81 (cm2).
Giải bài tập sách giáo khoa bài tính chất kết hợp của phép cộng lớp 4
Bài 1 (trang 45 SGK Toán 4)
Tính bằng cách thuận tiện nhất
a) 3254 + 146 + 1698.
4367 + 199 + 501.
4400+ 2148 + 252.
b) 921 + 898 + 2079 .
1255 + 436 + 145.
467 +999 + 9533.
Lời giải:
a ) 3254 + 146 + 1698 = 3400 + 1698
= 3400 + 1600 +98 = 5000+ 98
= 5098
4367 + 199 + 501 = 4367 + 700
= 4300 + 700 + 67 – 5000 + 67
= 5067
4400 + 2148 + 252 = 4400 + 2400 = 6800.
b) 921 + 898 + 2079 = 921 + 2079 + 898
= 3000 + 898 = 3989.
1255 + 436 + 145 = 1400 + 436 = 1836.
467 +999 +9533 = 10000+ 999 = 10999.
Bài 2 (trong 45 SGK Toán 4)
Một quỹ tiết kiệm ngày đầu nhận được 75.500 000 đồng, ngày thứ hai nhận được B6 950.000 đồng, ngày thứ ba nhận được 14.500.000 đồng. Hỏi có ba ngày quỹ tiết kiệm đó nhận được bao nhiêu tiền?
Lời giải:
Hai ngày đáo quỹ tiết kiệm nhận được số tiền là: 75.500.000 + 86.950.000 = 162.450.000 (đồng).
Cả ba ngày quỹ tiết kiệm nhận được số tiền là: 162.450.000 + 14.500.000 = 176.950.000 (đồng).
Đáp số: 176.950.000 (đồng).
Có thể tính nhẩm như sau :
75.500.000 + 14.500.000 + 86.950.000 = 90.000.000 + 86.950.000= 176.950.000 (đồng).
Bài 3 (trang 45 SGK Toán 4)
Viết số hoặc chữ thích hợp vớp chỗ chấm
a) a + 0 = …+ a =…
b ) 5 + a = … + 5
c) (a + 28) + 2 = a + (28 + …)= a + 30
Lời giải:
a) a + 0 = 0 + a = a
b) 5 + a = a + 5
c) (a + 28) + 2 = a + (28 +2)= a + 30
Trên đây là nội dung bài tính chất kết hợp của phép cộng. Chúng Tôi đã hướng dẫn giải các bài tập một cách cụ thể và dễ hiểu đến với các bạn học sinh. Các bạn cảm thấy bài toán thế nào? Hãy để comment phía bên dưới nhé!
Kết hợp là tính chất quan trọng của phép cộng trong toán học. Tính chất này giúp chúng ta thực hiện các phép tính cộng một cách linh hoạt và tương đồng, đồng thời cho phép chúng ta áp dụng phép cộng trên các tập hợp lớn hơn.
Theo tính chất kết hợp, khi ta cộng ba số hạng bất kỳ, kết quả không thay đổi dù ta thực hiện cộng từ phải sang trái hay từ trái sang phải. Ví dụ, cho ba số hạng a, b và c, ta có (a + b) + c = a + (b + c). Đây là một quy tắc quan trọng trong phép cộng và nó giúp ta thực hiện các phép tính cộng một cách dễ dàng và nhanh chóng.
Tính chất kết hợp của phép cộng cũng cho phép chúng ta áp dụng phép cộng trên các tập hợp lớn hơn như các tập hợp các số nguyên, các số thực hay các ma trận. Việc áp dụng phép cộng trên các tập hợp này dựa trên tính chất kết hợp đã được chứng minh trong trường hợp căn bản.
Tóm lại, tính chất kết hợp là một tính chất quan trọng trong phép cộng. Nó giúp chúng ta thực hiện các phép tính cộng một cách linh hoạt và tương đồng, đồng thời cho phép chúng ta áp dụng phép cộng trên các tập hợp lớn hơn. Hiểu về tính chất này sẽ giúp chúng ta nắm vững phép cộng và ứng dụng nó trong các bài toán thực tế.
Cảm ơn bạn đã xem bài viết Tính chất kết hợp của phép cộng? Lời giải bài tập trong SGK tại Thcslytutrongst.edu.vn bạn có thể bình luận, xem thêm các bài viết liên quan ở phía dưới và mong rằng sẽ giúp ích cho bạn những thông tin thú vị.
Từ Khoá Liên Quan:
1. Phép cộng
2. Tính chất giao hoán
3. Tính chất kết hợp
4. Phần tử đơn vị
5. Tính chất kết hợp yếu
6. Tính chất kết hợp mạnh
7. Tính chất kết hợp dễ chứng minh
8. Tính chất kết hợp khái quát
9. Định nghĩa tính chất kết hợp
10. Sự khác nhau giữa tính chất kết hợp yếu và mạnh
11. Kỹ thuật chứng minh tính chất kết hợp
12. Công thức tính tổng các số liên tiếp
13. Cộng hai hai số lớn
14. Cộng các số hạng trong dãy
15. Cách tính tổng của các số nguyên.


