Bạn đang xem bài viết Tính chất lục giác đều là gì? 3 ứng dụng của lục giác đều trong cuộc sống tại Thcslytutrongst.edu.vn bạn có thể truy cập nhanh thông tin cần thiết tại phần mục lục bài viết phía dưới.
Lục giác đều là một hình học đặc biệt với các tính chất độc đáo, thu hút sự quan tâm của nhiều người. Tuy có thể xuất hiện trong nhiều lĩnh vực khác nhau, nhưng lục giác đều vẫn tồn tại như một khái niệm chung trong toán học và hình học.
Tính chất cơ bản của lục giác đều là các cạnh và góc nội tiếp đều. Điều này có nghĩa là tất cả các cạnh của lục giác có cùng độ dài và tất cả các góc nội tiếp đều có cùng một giá trị, trong trường hợp này là 120 độ. Điều này tạo ra một cấu trúc đối xứng và đẹp mắt, và làm cho lục giác đều trở thành một hình dạng hấp dẫn và phổ biến.
Với những tính chất đặc biệt này, lục giác đều đã tìm thấy ứng dụng trong nhiều lĩnh vực khác nhau của cuộc sống. Đầu tiên, lục giác đều được sử dụng rộng rãi trong kiến trúc và xây dựng. Bởi vì tính đều và đối xứng của nó, lục giác đều thường được sử dụng làm cơ sở cho việc xây dựng các cấu trúc mạnh mẽ và ổn định như cầu, các tòa nhà và tháp nước.
Thứ hai, lục giác đều cũng được áp dụng trong thiết kế công nghiệp và sản xuất. Ví dụ, trong ngành công nghiệp hàng không, các phi cơ đôi khi được thiết kế với dạng hình lục giác đều để tối đa hóa hiệu suất và khả năng chịu tải. Sự đều đặn và đối xứng của lục giác đều cũng đóng vai trò quan trọng trong việc chế tạo các loại hình học khác như van, bánh răng và các thành phần máy móc khác.
Cuối cùng, lục giác đều còn được sử dụng trong nghệ thuật và sáng tạo. Hình dạng đẹp mắt và sự đều đặn của lục giác đều đã trở thành nguồn cảm hứng cho nhiều nghệ sĩ và thiết kế để tạo ra các tác phẩm nghệ thuật, trang trí và đồ họa. Ví dụ, hình lục giác thường được sử dụng để tạo ra các mẫu hình trang trí hoặc lưới trong đồ gốm, gạch men, thảm trải sàn…
Tóm lại, tính chất đặc biệt của lục giác đều đã tạo nên sự ưu ái và sự quan tâm của nhiều người. Từ kiến trúc, sản xuất đến nghệ thuật, lục giác đều đóng vai trò quan trọng trong cuộc sống của chúng ta và có nhiều ứng dụng đa dạng.
Hình lục giác là một hình học đặc biệt trong cấu trúc hình học. Hình lục giác được ứng dụng khá rộng rãi trong tính toán thực tế. Cùng Chúng Tôi tìm hiểu tính chất lục giác đều ngay nhé!
Lục giác đều là gì?
Hình lục giác là gì?
Hình lục giác hoặc hình sáu cạnh là một đa giác, một hình thể trong hình học phẳng. Hình lục giác bao gồm sáu góc và sáu cạnh.
Tính chất lục giác đều gồm những đặc điểm nào cùng Chúng Tôi tham khảo tiếp nhé!

Lục giác đều là gì?
Lục giác đều là hình có 6 cạnh đều và có chiều dài bằng nhau. Chỉ khi nào hình lục giác có 6 cạnh và 5 góc bằng nhau thì mới được gọi là hình lục giác đều. Đồng thời, một hình khối với hai đáy hình lục giác gọi là lục lăng.
Qua những khái niệm trên chắc hẳn, độc giả đã hiểu phần nào về hình lục giác. Cùng Chúng Tôi khám phá tiếp đến tính chất lục giác đều là gì nhé!
Đặc điểm, tính chất hình lục giác đều
Hình lục giác đều còn mang những đặc điểm, tính chất lục giác đều như sau:
- Hình lục giác đều bao gồm 6 hình tam giác đều.
- Các cạnh bằng nhau và các góc ở đỉnh bằng nhau.
- Tâm của đường tròn ngoại (và nội) tiếp là tâm đối xứng quay (tỏa tròn).
- Các cạnh của nó dài đúng bằng bán kính đường tròn ngoại tiếp.
- Bán kính của đường tròn ngoại tiếp sẽ bằng với chiều dài của cạnh lục giác.
- Các cạnh liền kề nhau trong hình lục giác đều tạo thành 1 góc 120 độ.
Công thức tính lục giác đều
Công thức tính diện tích lục giác đều
Để tính được diện tích của hình lục giác đều, ta sử dụng công thức như sau:
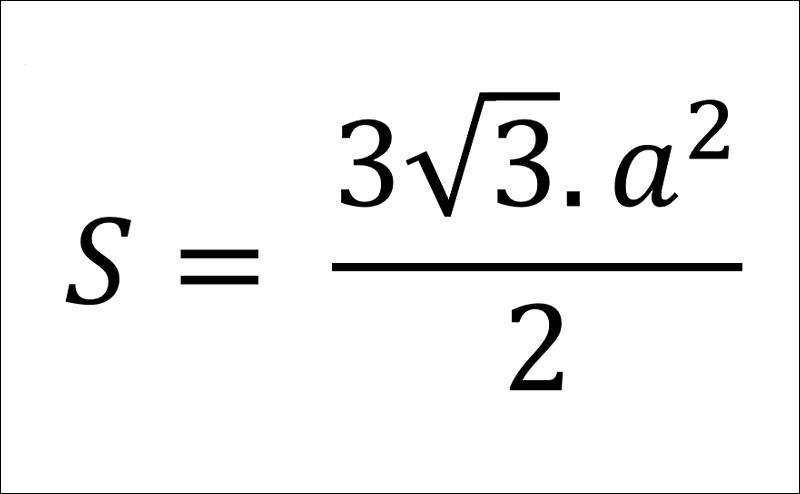
Trong đó:
- S là kí hiệu diện tích.
- a là độ dài cạnh của lục giác.
Công thức tính thể tích lục giác đều
Để tính được thể tích của hình lục giác đều, ta sử dụng 2 công thức như sau:
Công thức số 1: V = h * s
Trong đó: Chiều cao h và diện tích cơ sở S.
Công thức số 2: V = 3 * 3/2 * h * a mũ 2
Trong đó: Chiều cao h và chiều dài của cạnh bằng a.
Công thức tính chu vi lục giác đều
Để tính được chu vi của hình lục giác đều, ta sử dụng công thức như sau:
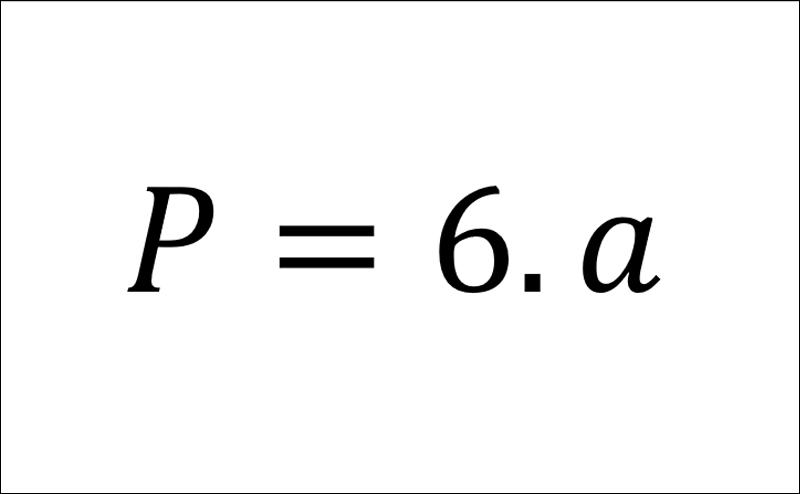
Trong đó:
- P: Chu vi.
- a: Độ dài một cạnh.
Hướng dẫn cách vẽ lục giác đều
Từ tính chất lục giác đều, ta có thể vẽ hình lục giác đều bằng compa, bạn hãy thực hiện theo các bước sau:
Bước 1: Trước tiên, bạn hãy vẽ 1 đường tròn C có bán kính bất kỳ.
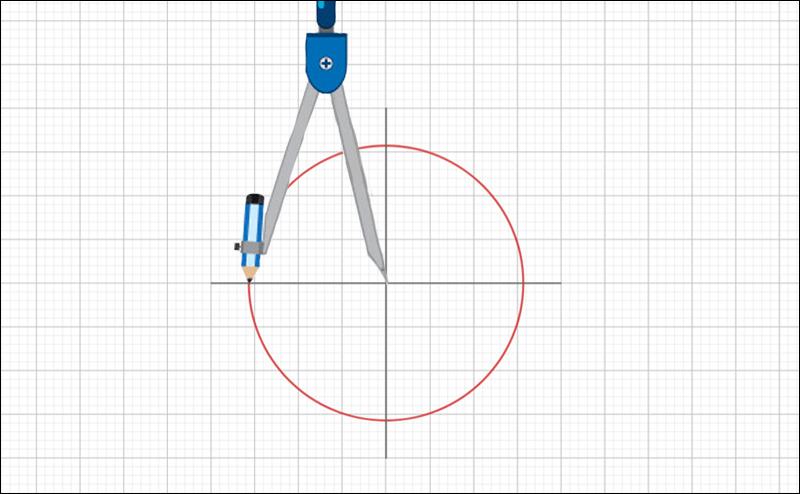
Bước 2: Đặt tâm của compa nằm trên đường tròn C. Sau đó, quay các đường tròn khác đồng tâm với đường tròn C, đỉnh của hình lục giác đều chính là điểm cắt với hình tròn C.
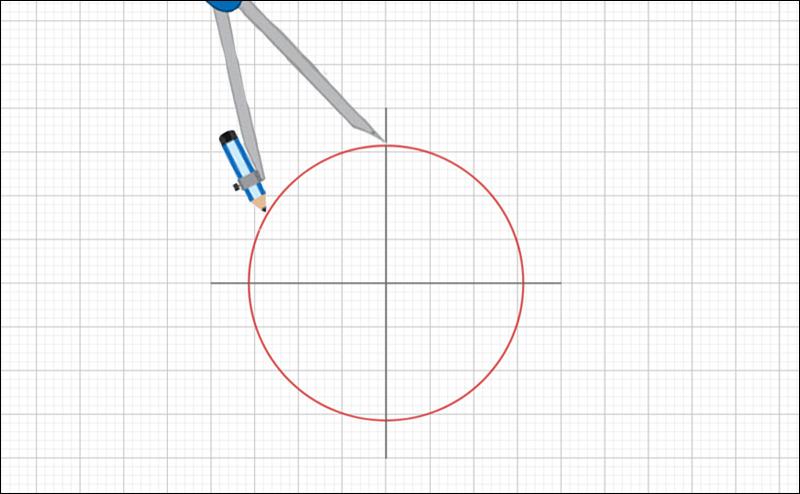
Bước 3: Tâm của đường tròn sau là giao điểm của đường tròn C với đường tròn trước đó.
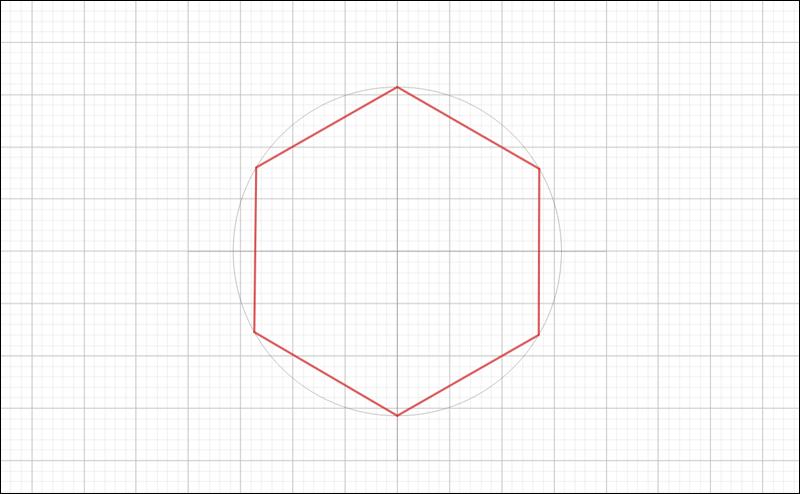
Bài tập liên quan tính chất lục giác đều
Sau khi ôn lại kiến thức về khái niệm và tính chất lục giác đều. Thì cùng Chúng Tôi củng cố lại kiến thức qua một số bài tập minh hoạ về tính chất lục giác đều ngay nhé!
Bài 6 trang 156 SBT Toán 8 Tập 1: Áp dụng tính chất lục giác đều:
a. Vẽ hình và tính số đường chéo của ngũ giác, lục giác.
b. Chứng minh rằng hình n – giác có tất cả (n(n-3))/3 đường chéo.
Hướng dẫn giải bài tập:
a. Áp dụng tính chất lục giác đều. Ta có từ mỗi đỉnh của ngũ giác vẽ được 2 đường chéo. Ngũ giác có 5 đỉnh ta kê được 5.2=10 đường chéo. Trong đó mỗi đường chéo được tính hai lần. Vậy ngũ giác có tất cả 5 đường chéo.
Từ mỗi đỉnh của lục giác vẽ được 3 đường chéo. Lục giác có 6 đỉnh ta kẻ được 6.3 = 18 đường chéo. Trong đó mỗi đường chéo được tính hai lần. Vậy lục giác có tất cả 9 đường chéo.
b) Từ mỗi đỉnh của n-giác (lồi) vẽ được đoạn thẳng nối đỉnh đó với (n-1) đỉnh còn lại của đa giác, trong đó có 2 đoạn thẳng trùng với hai cạnh của đa giác. Vậy, qua mỗi đỉnh của n-giác (lồi) vẽ được (n−3) đường chéo.
Hình n-giác có n đỉnh nên vẽ được đường chéo. Trong đó mỗi đường chéo được tính hai lần.
Vậy, hình giác có tất cả ( đường chéo.
Hoạt động 3: Trang 78 Toán 6 tập 1 sgk chân trời sáng tạo
a. Các em ghép các tam giác đều theo hướng dẫn để được hình 3.
b. Từ tính chất lục giác đều hãy nhận xét: Các góc và các cạnh của tam giác đều bằng nhau.
Vận dụng: Trang 78 Toán 6 tập 1 sgk chân trời sáng tạo
Áp dụng tính chất lục giác đều thì ta kết luận rằng bạn Bình đúng.
Bởi vì: Nếu hình có sáu cạnh có chiều dài bằng nhau, nó được gọi là một hình lục giác sáu cạnh đều. Chỉ khi tất cả các góc có cùng kích thước và các cạnh bằng nhau, mới gọi là lục giác đều.
Một số ứng dụng của lục giác đều trong cuộc sống
Sau đây là một số ứng dụng tính chất lục giác đều trong cuộc sống hiện nay. Cùng Chúng Tôi chiêm ngưỡng nhé!
Các lỗ tổ ong mật có hình lục giác đều
Tổ ong là do rất nhiều lỗ với hình dạng to nhỏ không giống nhau tạo thành. Nhìn qua từ bên trên, chúng là hình lục giác đều, nhưng sắp xếp rất có trật tự. Nhưng nếu nhìn từ bên trái, chúng lại do rất nhiều hình lăng trụ lục giác đều ghép lại với nhau.
Mà đáy của mỗi hình lăng trụ lục giác đều lại càng làm cho con người ta kinh ngạc. Nó không phẳng, cũng không phải tròn. Mà là nhọn, là do ba lăng trụ đáy nhọn hoàn toàn giống nhau hợp thành.

Qua vài thế kỷ nghiên cứu kết cấu của tổ ong. Con người phát hiện ra kết cấu này có lợi nhất cho việc tiết kiệm nhiên liệu và tận dụng không gian. Con người còn tìm ra không ít những vận dụng diệu kỳ của nó.
Hiện nay con người đang ứng dụng rộng rãi tính chất lục giác đều trong các lĩnh vực như kiến trúc, hàng không, vô tuyến điện,… Từ kiến trúc “Tầng hầm kiểu tổ ong” cách âm cách điệu đến thiết kế con tàu con thoi phóng vào vũ trụ, đều quan hệ mật thiết với kết cấu của tổ ong.
Nước Pháp là “đất nước hình lục giác”
Người Pháp gọi đất nước của họ với cái tên trìu mến “L’Hexagone” (tạm dịch là hình lục giác), do hình dạng địa lý đặc biệt của nó. Nhìn từ bản đồ thế giới, Pháp trông giống như một hình lục giác hay khiến người ta liên tưởng đến ngôi sao năm cánh.

Pháp có biên giới chung với rất nhiều nước như Bỉ, Luxembourg, Đức, Thụy Sĩ, Ý, Monaco, Andorra và Tây Ban Nha. Tất nhiên, hình lục giác chỉ bao gồm đất liền. Bởi ngoài ra, Pháp còn có Corsica và các vùng lãnh thổ hải ngoại khác.
Hình lục giác là hình khối phổ biến trong xây dựng lăng mộ
Tính chất lục giác đều có ý nghĩa hướng về tự nhiên. Hình lục giác là biểu tượng của vẻ đẹp hoàn hảo. Mộ đá lục lăng được xây dựng trên ý tưởng của hình lục giác.
Nó gồm có 6 cạnh đều nhau được gọi là 6 bưng bên che phủ phần mộ. Mộ đá được xây dựng trên hình khối này tiết kiệm được nhiều nguyên vật liệu nhưng vẫn rất bền chắc và thiên về tự nhiên.
Chúng Tôi hi vọng với những kiến thức chia sẻ trên đây sẽ hữu ích đối với độc giả. Đặc biệt là các em học sinh trong quá trình làm bài tập ở nhà cũng như khi học trên lớp. Hãy cùng Chúng Tôi cập nhật những nội dung mới nhất mỗi ngày nhé!
Tính chất lục giác đều là gì? 3 ứng dụng của lục giác đều trong cuộc sống
Kết luận
Lục giác đều là một hình học có 6 cạnh và 6 góc bằng nhau. Tính chất lục giác đều có ảnh hưởng rất sâu sắc trong nhiều lĩnh vực của cuộc sống và mang lại những ứng dụng quan trọng. Ba ứng dụng phổ biến của lục giác đều trong cuộc sống là trong kiến trúc, công nghệ và tự nhiên.
Trước hết, lục giác đều được sử dụng rộng rãi trong kiến trúc. Đặc điểm của nó góp phần làm nổi bật và tạo nên hiệu ứng thị giác đặc biệt cho các tòa nhà và công trình xây dựng. Với hình dáng đồng đều và cân đối, lục giác đều tạo nên một cảm giác ổn định và đẹp mắt. Nó có thể thấy rõ ràng trong các công trình nổi tiếng như Tòa nhà Louvre ở Paris, Nhà thép Möller Villa ở Đức và Nhà hát Sydney ở Úc.
Thứ hai, lục giác đều cũng được áp dụng rộng rãi trong công nghệ. Hình dạng lục giác đều ổn định và mạnh mẽ, cho phép nó được sử dụng trong nhiều thiết kế kỹ thuật. Một ví dụ điển hình là trong ngành hàng không vũ trụ, các cấu trúc dạng lục giác đều được sử dụng để tạo ra khung sườn cứng và nhẹ cho tàu vũ trụ và tàu con thoi. Lục giác đều cũng thường xuyên xuất hiện trong các thiết kế máy bay và đường ống dẫn dầu.
Cuối cùng, lục giác đều xuất hiện tự nhiên trong nhiều hiện tượng tự nhiên và cơ thể sống. Chẳng hạn, tổ ong có hình dáng lục giác đều, được xây dựng cẩn thận và có thể tồn tại trong thời gian dài. Lục giác đều cũng xuất hiện trong một số phân tử, ví dụ như hạt ngô và tinh thể băng. Bởi vì hình dạng này cung cấp sự cân đối và sắp xếp gọn gàng, nên lục giác đều tồn tại rất phổ biến trong tự nhiên.
Tóm lại, tính chất lục giác đều có sự ảnh hưởng rất rộng rãi trong cuộc sống. Từ kiến trúc đến công nghệ và tự nhiên, lục giác đều đóng vai trò quan trọng trong việc tạo ra những thiết kế cân bằng và ổn định. Việc hiểu và tận dụng tính chất của hình dạng này sẽ mang lại nhiều lợi ích trong xã hội và cuộc sống hàng ngày của chúng ta.
Cảm ơn bạn đã xem bài viết Tính chất lục giác đều là gì? 3 ứng dụng của lục giác đều trong cuộc sống tại Thcslytutrongst.edu.vn bạn có thể bình luận, xem thêm các bài viết liên quan ở phía dưới và mong rằng sẽ giúp ích cho bạn những thông tin thú vị.
Từ Khoá Liên Quan:
1. Lục giác đều là gì
2. Đặc điểm của lục giác đều
3. Công thức tính diện tích lục giác đều
4. Công thức tính chu vi lục giác đều
5. Các gọi khác của lục giác đều
6. Đường kính đường tròn ngoại tiếp lục giác đều
7. Đường kính đường tròn nội tiếp lục giác đều
8. Tính chất của các góc trong lục giác đều
9. Công thức tính cạnh lục giác đều khi biết diện tích
10. Công thức tính cạnh lục giác đều khi biết chu vi
11. Ứng dụng lục giác đều trong kiến trúc
12. Ứng dụng lục giác đều trong ngành công nghiệp
13. Ứng dụng lục giác đều trong công nghệ thông tin
14. Sự tồn tại và ứng dụng của lục giác đều trong tự nhiên
15. Ví dụ về ứng dụng của lục giác đều trong cuộc sống hàng ngày.


