Bạn đang xem bài viết Tính chất trọng tâm tam giác và cách xác định trọng tâm tại Thcslytutrongst.edu.vn bạn có thể truy cập nhanh thông tin cần thiết tại phần mục lục bài viết phía dưới.
Trọng tâm tam giác là một điểm đặc biệt, nằm trong tam giác, và có vai trò quan trọng trong nhiều bài toán và ứng dụng của hình học. Tính chất của trọng tâm tam giác không chỉ đơn giản trong việc tính toán mà còn có ảnh hưởng sâu sắc đến các khía cạnh khác nhau trong toán học và cả trong thực tế.
Trọng tâm tam giác là điểm cân bằng của tam giác, tức là nếu treo tam giác lên bằng một sợi dây từ trọng tâm, tam giác sẽ không bị lệch về phía nào. Điều này có nghĩa là trọng tâm tam giác chia tam giác thành ba phần có diện tích bằng nhau.
Cách xác định trọng tâm tam giác cũng rất đơn giản. Đầu tiên, ta cần biết vị trí của ba đỉnh A, B và C của tam giác. Sau đó, ta kết nối các đỉnh này với nhau và tìm giao điểm của ba đường thẳng này. Điểm giao điểm chính là trọng tâm tam giác.
Trọng tâm tam giác có rất nhiều ứng dụng trong đời sống thực tế và các lĩnh vực khác nhau. Ví dụ, trong kiến trúc, trọng tâm tam giác thường được sử dụng để tính toán tải trọng và định vị các cột, móng đỡ và các cấu trúc khác. Ngoài ra, trong thiết kế và sản xuất, trọng tâm tam giác cũng được áp dụng để xác định điểm trung tâm và cân bằng cho các đối tượng như bánh xe, máy móc và các sản phẩm công nghệ khác.
Tóm lại, tính chất của trọng tâm tam giác và cách xác định nó rất quan trọng trong lĩnh vực toán học và ứng dụng thực tế. Việc hiểu và áp dụng tốt tính chất này sẽ giúp chúng ta giải quyết nhiều bài toán phức tạp và tạo ra các giải pháp hiệu quả trong các lĩnh vực khác nhau.
Trong Toán học phổ thông, chúng ta đã được học về trọng tâm của tam giác. Vậy tính chất trọng tâm tam giác là gì? Có những cách nào để xác định tính chất trọng tâm tam giác? Mời các bạn đọc của Chúng Tôi cùng tìm hiểu ngay sau đây.
Tính chất trọng tâm tam giác
Trọng tâm tam giác là gì?
Trước khi tìm hiểu tính chất trọng tâm tam giác là gì, chúng ta cần biết được khái niệm về trọng tâm tam giác. Trọng tâm tam giác là giao điểm của ba đường trung tuyến của tam giác đó.
Đường trung tuyến của một tam giác chính là đoạn thẳng nối từ một đỉnh đến trung điểm của cạnh đối diện.
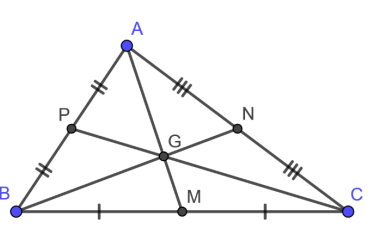
Ví dụ: Tam giác ABC có các đường trung tuyến AM, BN, CP cùng đi qua G.
Điểm G được gọi là trọng tâm tam giác ABC.
Tính chất trọng tâm tam giác
Tính chất của trọng tâm tam giác là: Khoảng cách từ trọng tâm tới 3 đỉnh của tam giác bằng 2/3 độ dài đường trung tuyến ứng với đỉnh đó.
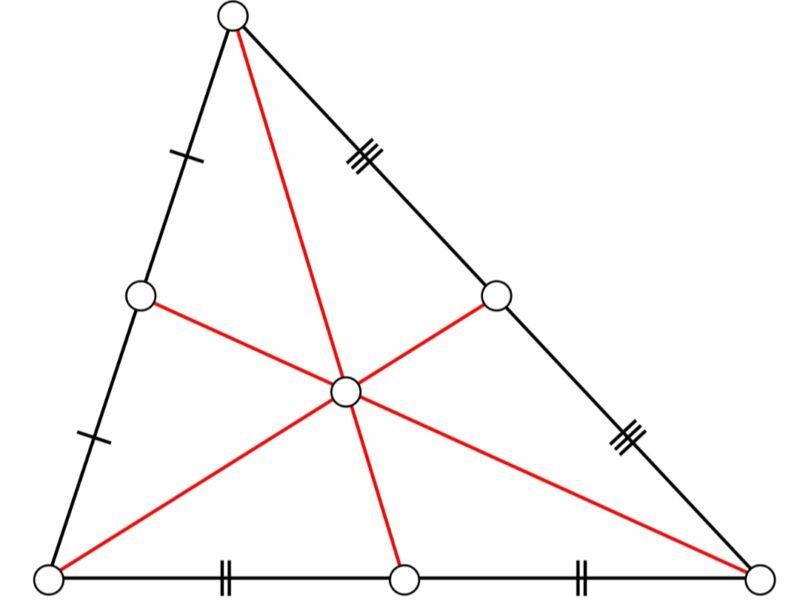
Giả sử, tam giác ABC có 3 đường trung tuyến là AM, BN, CP với G là trọng tâm như hình. Theo tính chất trên, ta có:
- GA = 2/3 AM
- GB = 2/3 AN
- GC = 2/3 CP
Ngoài ra, chúng ta còn một số hằng đẳng thức khác liên quan đến trọng tâm tam giác. Xét theo khía cạnh, điểm G chia mỗi đường trung tuyến thành 3 phần bằng nhau.
- Đối với đường trung tuyến AM, ta có:
AM = 3 GM; AM = 3/2 AG; AG = 2 GM; GM = 1/2 AG,…
- Đối với đường trung tuyến BN, ta có:
BN = 3 GN; BN = 3/2 BG; BG = 2 GN; GN = 1/2 BG,…
- Đối với đường trung tuyến CP, ta có:
CP = 3 GP; CP = 3/2 CG; CG = 2 GP; GP = 1/2 CG,…
Chủ đề liên quan:
- Tính chất đường trung trực của một đoạn thẳng
- Tính chất trọng tâm của tam giác
Cách xác định trọng tâm tam giác
Để xác định trọng tâm của một tam giác, ta có thể thực hiện theo hai cách sau:
Cách 1
Cho tam giác ABC.
Xác định trung điểm M của cạnh BC sao cho MB = MC.
Nối A với M để có đường trung tuyến AM.
Thực hiện tương tự với các cạnh và đỉnh còn lại, chúng ta sẽ có thêm hai đường trung tuyến nữa của tam giác này.
Gọi giao điểm của ba đường trung tuyến là G. Khi đó, điểm G chính là trọng tâm tam giác ABC.
Cách 2
Cho tam giác ABC.
Xác định trung điểm M của cạnh BC sao cho MC = MB.
Nối đỉnh A với điểm M ta được đường trung tuyến AM.
Trên đoạn thẳng AM, lấy một điểm G sao cho: AG = 2/3 AM.
Theo tính chất trọng tâm tam giác, điểm G chính là trọng tâm tam giác ABC.
Tính chất trọng tâm tam giác khác
Tính chất trọng tâm tam giác vuông
Tính chất trọng tâm tam giác vuông cũng giống như tam giác thường.
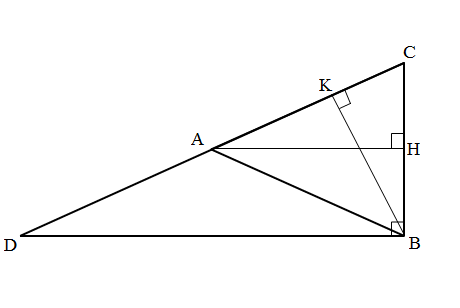
Tam giác ABC vuông tại B, từ B vẽ đường trung tuyến BA. Ta có, BA là đường trung tuyến của góc vuông nên BA = 1/2 CD = AD = AC.
Vậy tam giác ADB và tam giác ABC lần lượt cân tại A.
Tính chất trọng tâm tam giác cân
Tính chất trọng tâm tam giác cân cũng giống với tam giác thường.
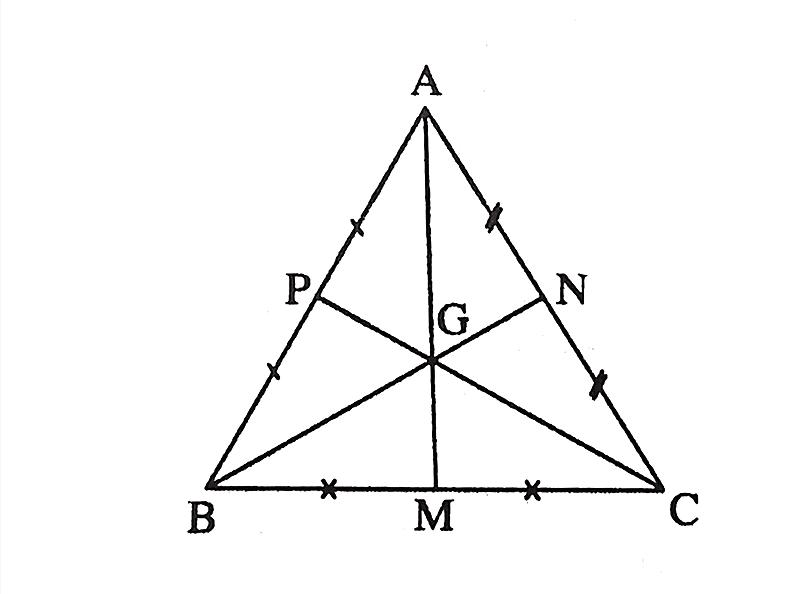
Xét tam giác ABC cân tại A với G là trọng tâm. Khi đó, AG vừa là đường trung tuyến, vừa là đường phân giác và là đường cao của tam giác ABC này.
Ta có: AG vuông góc với BC. Suy ra, tam giác ACI và ABI lần lượt vuông tại I.
Tính chất trọng tâm tam giác đều
Tính chất trọng tâm tam giác đều cũng giống tam giác thường.
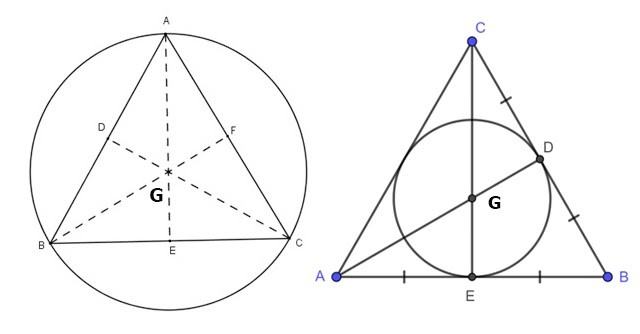
Xét tam giác đều ABC với G là giao điểm của 3 đường trung tuyến xuất phát từ 3 đỉnh. Khi đó, G vừa là trọng tâm, trực tâm, tâm đường tròn nội tiếp, tâm đường tròn ngoại tiếp của tam giác đều ABC.
Bài tập vận dụng về tính chất trọng tâm tam giác
Bài tập 1: Cho tam giác ABC có trọng tâm G. Biết AM là đường trung tuyến với M thuộc cạnh BC và AM = 12cm. Tính độ dài đoạn AG và GM?
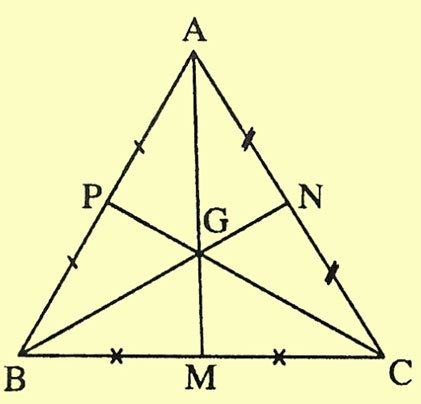
Lời giải:
Ta có: G là trọng tâm tam giác ABC. Áp dụng ính chất trọng tâm tam giác nên suy ra:
AG = 2/3 AM = 2/3 . 12 = 8 (cm)
GM = 1/3 AM = 1/3 . 12 = 4 (cm)
Vậy độ dài đoạn AG là 8cm và đoạn GM là 4cm.
Bài tập 2: Cho tam giác ABC, trung tuyến BM = CN. BM cắt CN tại G. Chứng minh tam giác ABC cân tại A.
Lời giải:
Vì BM và CN là hai đường trung tuyến của tam giác mà BM giao CN tại G, áp dụng tính chất trọng tâm tam giác nên ta có:
BG/BM = CG/CN = 2/3
mà BM = CN nên BG = CN và GN = GM;
Xét tam giác BNG và tam giác CGM ta có:
BG = CN; GN = GM
Góc BGN = góc CGM ( 2 góc đối đỉnh)
Suy ra, tam giác BNG đồng dạng tam giác CMG
Từ đó suy ra: BN = CM (1)
mà M và N lần lượt là trung điểm của AB và AC (2)
Từ (1) và (2) ta có: AB = AC => Tam giác ABC cân tại A( đpcm).
Thông qua bài viết trên, chúng ta đã biết được tính chất trọng tâm tam giác và cách xác định trọng tâm của tam giác. Chúng Tôi hi vọng các bạn đã có thêm cho mình những kiến thức Toán học thú vị. Đừng quên theo dõi chúng tôi trong các bài viết tiếp theo.
Kiến thức cơ bản: Tính chất của tam giác cân
Tính chất trọng tâm của tam giác là một trong những đặc điểm quan trọng và hữu ích trong lĩnh vực hình học và tính toán. Trọng tâm tam giác được xác định bằng cách giao điểm của ba đường trung tuyến của tam giác.
Một trong những tính chất quan trọng của trọng tâm tam giác là trọng tâm chia tam giác thành ba phần có diện tích bằng nhau. Điều này có nghĩa rằng, nếu chúng ta vẽ các đường thẳng từ trọng tâm đến các đỉnh của tam giác, thì các phần tam giác được chia thành sẽ có diện tích bằng nhau.
Thêm vào đó, trọng tâm cũng là trung điểm của các đoạn thẳng nối các đỉnh của tam giác đến trọng tâm. Điều này có nghĩa là, từ mỗi đỉnh của tam giác, ta cần đi qua trọng tâm để đến được các đỉnh còn lại, và khoảng cách từ trọng tâm đến mỗi đỉnh là bằng nhau.
Cách xác định trọng tâm của tam giác cũng rất đơn giản. Đầu tiên, ta vẽ hai đường thẳng từ hai đỉnh của tam giác để nối chúng với trung điểm của cạnh đối diện. Tiếp theo, ta vẽ đường thẳng từ trung điểm của một cạnh bất kỳ đến giao điểm của hai đường thẳng đã vẽ trước đó. Điểm giao điểm của ba đường thẳng này chính là trọng tâm của tam giác.
Trọng tâm tam giác là một điểm quan trọng có nhiều ứng dụng trong hình học, cơ học, và địa hình. Nó có thể giúp ta tính toán diện tích, tọa độ và các thuộc tính khác của tam giác một cách dễ dàng.
Cảm ơn bạn đã xem bài viết Tính chất trọng tâm tam giác và cách xác định trọng tâm tại Thcslytutrongst.edu.vn bạn có thể bình luận, xem thêm các bài viết liên quan ở phía dưới và mong rằng sẽ giúp ích cho bạn những thông tin thú vị.
Từ Khoá Liên Quan:
1. Trọng tâm tam giác
2. Xác định trọng tâm tam giác
3. Tính chất của trọng tâm tam giác
4. Trọng tâm tam giác đồng nhất
5. Trọng tâm tam giác cân
6. Trọng tâm tam giác vuông
7. Trọng tâm tam giác không đều
8. Công thức tính tọa độ trọng tâm tam giác
9. Cách xác định trọng tâm tam giác bằng phương trình đồ thị
10. Tính chất liên quan đến trọng tâm tam giác trong hình học
11. Định nghĩa trọng tâm tam giác
12. Đặc điểm của trọng tâm tam giác
13. Tọa độ của trọng tâm tam giác
14. Phương trình tính trọng tâm tam giác
15. Ứng dụng của trọng tâm tam giác trong giải toán.


