Bạn đang xem bài viết Z là gì trong Toán học? Tìm hiểu các tập hợp số cơ bản khác tại Thcslytutrongst.edu.vn bạn có thể truy cập nhanh thông tin cần thiết tại phần mục lục bài viết phía dưới.
Toán học là một ngành khoa học nghiên cứu về các khái niệm, công thức và quy tắc để giải quyết các vấn đề liên quan đến số học, hình học, đại số và các lĩnh vực khác. Trong Toán học, “Z” đại diện cho tập hợp số nguyên. Tập hợp này bao gồm tất cả các số nguyên dương, số 0 và các số nguyên âm.
Trong toán học còn có các tập hợp số cơ bản khác như tập hợp số tự nhiên (N), tập hợp số nguyên không âm (N*), tập hợp số hữu tỉ (Q), tập hợp số vô tỉ (I) và tập hợp số thực (R).
Tập hợp số tự nhiên (N) bao gồm tất cả các số không âm, bắt đầu từ 0 và không có giới hạn về trên. Vì vậy, N = {0, 1, 2, 3, 4, …}.
Tập hợp số nguyên không âm (N*) bao gồm tất cả các số tự nhiên, bắt đầu từ 1 và không có giới hạn về trên. Dễ hiểu hơn, N* = {1, 2, 3, 4, …}.
Tập hợp số hữu tỉ (Q) bao gồm tất cả các số có thể biểu diễn dưới dạng phân số, trong đó tử số và mẫu số đều là số nguyên và mẫu số khác 0. Ví dụ, Q = {1/2, 2/3, -3/5, 0/1, …}.
Tập hợp số vô tỉ (I) bao gồm tất cả các số không thể biểu diễn dưới dạng phân số và không thể viết thành một số nguyên. Ví dụ, I = {√2, π, e, …}.
Tập hợp số thực (R) bao gồm tất cả các số có thể biểu diễn trên một trục số thực. Nó bao gồm cả tập hợp số hữu tỉ và tập hợp số vô tỉ, cũng như các số nguyên. Kí hiệu của tập hợp số thực là R.
Việc hiểu và nắm vững các tập hợp số cơ bản này trong toán học là cực kỳ quan trọng, vì chúng đóng vai trò quan trọng trong việc xây dựng cơ bản và thuật ngữ trong lĩnh vực này. AI can chi tiết kể rõ hơn về chủ đề này
Chắc hẳn ở những ngày đầu vào lớp 6, bạn đã quen với khái niệm tập hợp. Trong Toán lớp 10 bạn sẽ gặp lại kiến thức này. Bài viết hôm nay của Chúng Tôi sẽ giúp bạn nhắc nhớ khái niệm Z là gì trong Toán học.
Z là gì trong Toán học?
Z là gì trong Toán học?
Trong Toán học, Z là ký hiệu của tập hợp số nguyên. Tập hợp Z bao gồm số nguyên dương, số nguyên âm và cả số 0. Tập hợp Z còn có tên gọi khác là số nguyên.
Tập hợp số nguyên dùng để chỉ ra các số nguyên là miền xác định nguyên duy nhất. Trong đó các phần tử dương của nó được sắp thứ tự tốt và các thứ tự đó được bảo toàn dưới phép cộng. Cũng giống như các tập hợp số khác, tập hợp Z cũng là một tập hợp vô hạn.
Định nghĩa tập hợp Z
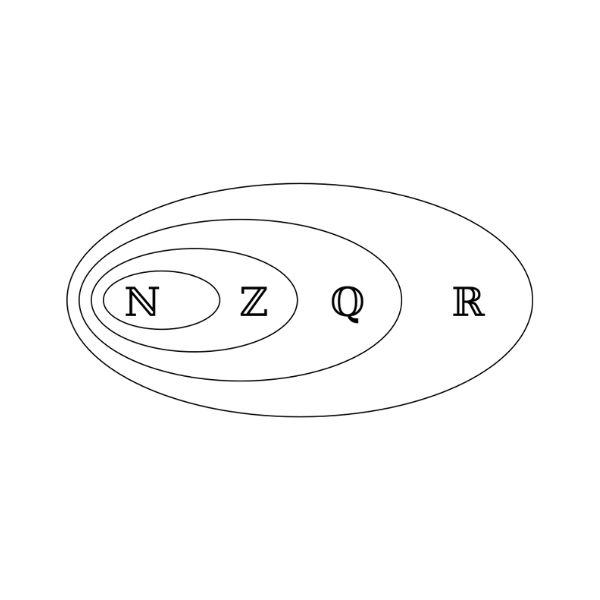
Tập hợp Z là tập hợp các số nguyên. Đây cũng là tập hợp con của hai tập hợp lớn hơn là tập hợp số hữu tỉ Q và số thực R. Bên cạnh đó, Z cũng là tập hợp mẹ của tập hợp số tự nhiên N.
Tập hợp số nguyên Z được chia thành hai tập hợp con là Z+ và Z-. Trong đó, Z+ là tập hợp các số nguyên dương lớn hơn 0. Z- là tập hợp các số nguyên âm nhỏ hơn 0. Đặc biệt, số 0 không nằm trong tập hợp con Z+ và Z-, nó chỉ năm tập hợp Z.
Tính chất của tập hợp Z
Dưới đây là một số tính chất của tập hợp Z:
- Trong tập hợp Z, không có số nguyên lớn nhất và số nguyên nhỏ nhất. Số nguyên nhỏ nhất và số nguyên lớn nhất chỉ mang tính chất tương đối và phụ thuộc vào điều kiện trong từng trường hợp xác định.
- Không tồn tại một số nguyên nào nằm giữa hai số nguyên liên tiếp.
Chắc hẳn qua phần thông tin trên bạn đọc đã nắm bắt được khái niệm Z là gì trong Toán học. Sau đây là phần bài tập về tập hợp Z để các bạn học sinh dễ dàng ghi nhớ hơn về kiến thức này. Mời bạn đọc theo dõi để biết thêm chi tiết.
Xem thêm:
- N là gì trong tiếng Anh? N là viết tắt từ gì trong tiếng Anh
- V là gì trong tiếng Anh? Giải thích nghĩa của từ viết tắt
Một số bài tập về tập hợp Z
Câu hỏi: Tính các biểu thức số nguyên sau:
A = (-37) + 14 + 26 + 37
B = (-24) + 6 + 10 + 24
C = 15 + 23 + (-25) + (-23)
D = 60 + 33 + (-50) + (-33)
E = (-16) + (-209) + (-14) + 209
F = (-12) + (-13) + 36 + (-11)
G = -16 + 24 + 16 – 34
H = 25 + 37 – 48 – 25 – 37
I = 2575 + 37 – 2576 – 29
J = 34 + 35 + 36 + 37 – 14 – 15 – 16 – 17
Trả lời:
A = 40
B = 16
C = -10
D = 10
E = -30
F = 0
G = -10
H = -48
I = 7
J = 80
Sau đây là phần nội dung cuối cùng của bài viết Z là gì trong Toán học. Đó là kiến thức về các tập hợp số cơ bản khác. Mời bạn đọc tham khảo cùng Chúng Tôi.
Các tập hợp số cơ bản khác
Dưới đây là các tập hợp số cơ bản khác:
Tập hợp số tự nhiên N:
N là kí hiệu của tập hợp số tự nhiên bao gồm các số như 0, 1, 2, 3,… Tập hợp số tự nhiên N là tập hợp số cơ bản nhỏ nhất trong hệ thống các tập hợp số.
N={0, 1, 2, 3, 4, 5, ..}.
Tập hợp số hữu tỉ Q:
Q là kí hiệu của tập hợp số hữu tỉ. Số hữu tỉ được biểu diễn bằng số thập phân hữu hạn hay số thập phân vô hạn tuần hoàn.
Q={ a/b; a, b∈Z, b≠0}

Tập hợp các số thực R:
R là kí hiệu của tập hợp các số thực R. Tập hợp của số thực R bao gồm các số hữu tỉ và các số vô tỉ. Số vô tỉ kí hiệu là I, được biểu diễn bằng một số thập phân vô hạn không tuần hoàn.
Mối quan hệ các tập hợp số
Trong Toán học, ta có:
R = Q ∪ I.
TA có: Tập hợp số N, Z, Q, R, I.
Mối quan hệ bao hàm giữa các tập hợp số là: N ⊂ Z ⊂ Q ⊂ R.
Cụ thể: N⊂ Z, Z ⊂ Q, Q ⊂ R, I ⊂ R, Q ∩ I = ∅.
Hi vọng qua bài viết trên, các bạn học sinh đã nắm vững được định nghĩa của tập hợp số và giải được các bài tập môn Toán về giao, phần bù, hiệu, hợp. Bên cạnh đó, bạn đọc hiểu được khái niệm Z là gì trong Toán học. Chúc các bạn hoàn thành tốt các bài tập trên lớp!
Trong lĩnh vực toán học, chúng ta thường gặp phải các loại tập hợp số cơ bản như N, Z, Q, R và C. Trong bài viết này, chúng ta đã tìm hiểu về tập hợp số Z và các tập hợp số cơ bản khác.
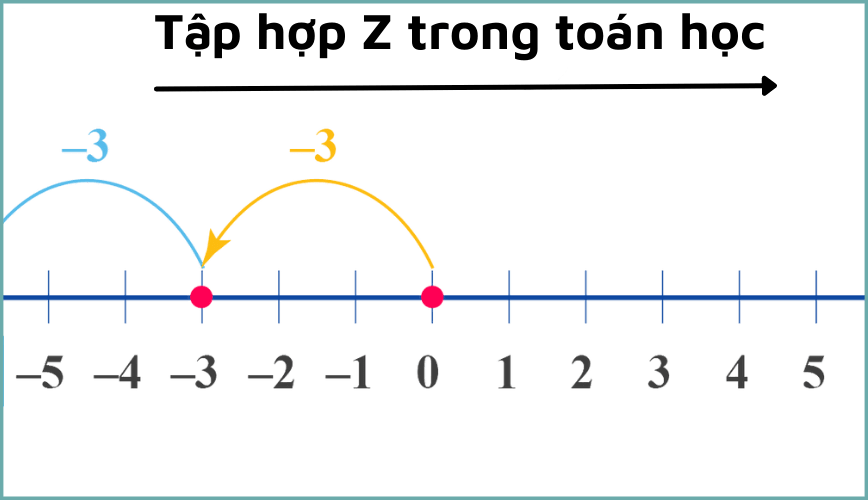
Tập hợp số Z, hay còn gọi là tập hợp số nguyên, bao gồm các số nguyên dương, số nguyên âm và số không. Điểm đặc biệt của tập hợp số Z là nó cung cấp khả năng biểu diễn vô hạn số số nguyên trên một trục số đơn giản. Sự phân biệt giữa số dương và số âm trên trục số giúp ta dễ dàng nhận biết tính chẵn lẻ của các số và thực hiện các phép tính cộng, trừ, nhân và chia.
Các tập hợp số cơ bản khác cũng đóng vai trò quan trọng trong toán học. Tập hợp số N là tập hợp các số tự nhiên, bắt đầu từ số 0 và không có giới hạn trên trục số dương. Tập hợp số Q gồm tất cả các số hữu tỉ, có thể biểu diễn dưới dạng phân số. Tập hợp số R bao gồm tất cả các số thực, bao gồm cả các số vô tỷ, và tập hợp số C là tập hợp các số phức.
Các tập hợp số cơ bản này không chỉ hữu ích trong toán học mà còn được áp dụng rộng rãi trong các lĩnh vực khác như vật lý, kỹ thuật và kinh tế. Sự hiểu biết về các tập hợp số này giúp chúng ta hiểu rõ hơn về cấu trúc và tính chất của số học.
Cảm ơn bạn đã xem bài viết Z là gì trong Toán học? Tìm hiểu các tập hợp số cơ bản khác tại Thcslytutrongst.edu.vn bạn có thể bình luận, xem thêm các bài viết liên quan ở phía dưới và mong rằng sẽ giúp ích cho bạn những thông tin thú vị.
Từ Khoá Liên Quan:
1. Z là gì trong Toán học
2. Z trong Toán học có nghĩa là gì?
3. Z là ký hiệu cho tập số nguyên trong Toán học
4. Định nghĩa và khái niệm về tập số nguyên Z
5. Các phép tính trong tập số nguyên Z
6. Ví dụ về số nguyên Z trong các bài toán Toán học
7. Các tính chất và đặc điểm của tập số nguyên Z
8. Tập số nguyên Z và tập số tự nhiên N có gì khác nhau?
9. Z+ và Z- trong tập số nguyên Z là gì?
10. Các tập hợp con của tập số nguyên Z
11. Tập số chẵn và số lẻ trong tập số nguyên Z
12. Tập số nguyên không âm và số nguyên dương trong Z
13. Tập số nguyên tố trong tập số nguyên Z
14. Phần tử lớn nhất và nhỏ nhất trong tập số nguyên Z
15. Sự hợp và giao của các tập con trong tập số nguyên Z


